Cho hình thang ABCD, AB là đáy nhỏ. Gọi M, N, P, Q lần lượt là trung điểm của AD, BC, BD và AC.
a) Chứng minh bốn điểm M, N, P, Q thẳng hàng;
 Giải bởi Vietjack
Giải bởi Vietjack
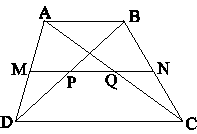
a) Xét ABD có MP là đường trung bình
Þ MP // AB Þ MP // CD.
Xét DADC có MQ là đường trung bình Þ MQ // CD.
Xét hình thang ABCD có MN là đường trung bình
=> MN // CD.
Qua điểm M có các đường thẳng MP, MQ, MN cùng song song với CD nên các đường thẳng này trùng nhau, suy ra bốn điểm M, N, P, Q thẳng hàng.
Cho hình thang ABCD (AB//CD), tia phân giác của góc C đi qua trung điểm M của cạnh bên AD. Chứng minh rằng:
a)Cho hình thang vuông ABCD tại A và D Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) cân tại F
Cho và đường thẳng d qua A không cắt đoạn thẳng BC. Vẽ . Gọi I là trung điểm của BC.Chứng minh ID = IE.
b, Gọi I là trung điểm của AB , đường thẳng vuông góc với IE tại E và đường thẳng vuông góc với IF tại F cắt nhau ở K. Chứng minh : KC = KD .
Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N.
a, Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.