Cho hình thang ABCD cân, đáy nhỏ AB và đáy lớn CD. Góc nhọn hợp bởi hai đường chéo AC, BD bằng . Gọi M và N là hình chiếu của B và C lên AC và BD, P là trung điểm cạnh BC. Chứng minh tam giác MNP là tam giác đều.
 Giải bởi Vietjack
Giải bởi Vietjack
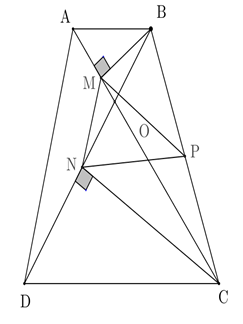
Xét tam giác và có DC chung, (gt), AD = BC (gt).
Suy ra: nên ( Cạnh tương ứng).
là tam giác cân, mà góc .
=> là tam giác đều.
Tương tự tam giác OAB là tam giác đều.
Ta có là các tam giác đều, BM, CN là các đường cao nên là trung tuyến.
Suy ra M là trung điểm OA, N là trung điểm OD. Do đó MN là đường trung bình của tam giác OAD (1)
Mặt khác PM, PN là các đường trung tuyến ứng với cạnh huyền BC của các tam giác vuông MBC và NBC nên (2)
Mà AD = BC (3)
Từ (1) (2) (3) suy ra: PM = PN = MN. Vậy tam giác MNP là tam giác đều.
Cho tam giác ABC cân tại A có AM là đường cao. N là trung điểm của AC. Kẻ Ax // BC cắt MN tại E. Chứng minh rằng:
a. ME // AB.
Cho tam giác ABC. Gọi M là trung điểm của BC, I là trung điểm của AM. Tia BI cắt AC ở D. Qua M kẻ đường thẳng song song với BD cắt AC ở E. Chứng minh:
a. AD = DE = EC.
Cho tam giác ABC cân tại A, đường trung tuyến CM và BN. Trên tia đối của tia BA lấy điểm D sao cho BD = AB. Chứng minh CD = 2CM.
Cho hình thang ABCD ( AB // CD, AB < CD). Trên AD lấy M, N, P sao cho AM = MN = NP = PQ. Từ M, N, P dựng các đường thẳng song song với hai đáy cắt BC lần lượt tại E, F, G. Chứng minh:
a. Chứng minh BE = EF = FG = GC.
Cho hình thang vuông ABCD, có . Gọi M, N lần lượt là trung điểm của các cạnh BC, AD. Chứng minh:
a. Tam giác MAD là tam giác gì? Vì sao?
Cho tam giác ABC có độ dài BC = 12cm và M là trung điểm của cạnh AB. Tia Mx song song với BC cắt AC tại N. Chứng minh:
a. N là trung điểm của cạnh AC.
Cho hình thang ABCD (AB // CD). E là trung điểm của AC, F là trung điểm của BD .đường thẳng EF // AB cắt BD tại Q, cắt BC tại Q.
a. Chứng minh PB = PD, QB = QC.