Cho tam giác vuông có . Dựng AD vuông góc với . Tia phân giác góc B cắt AC tại E.
Tính độ dài các đoạn thẳng AD,DB và DC.
 Giải bởi Vietjack
Giải bởi Vietjack
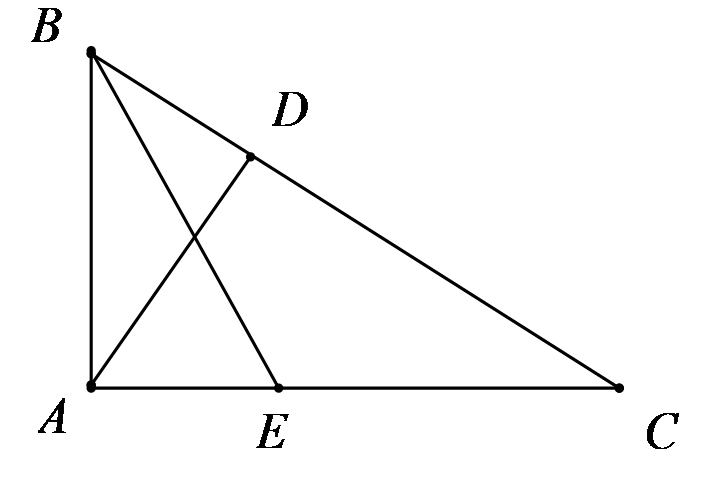
Áp dụng định lý Py-ta-go vào tam giác vuông ABC:
.
Xét và có:
(cùng phụ với )
góc chung
Do đó: (g.g)
Hay hay
Tính diện tích các tam giác ABD và ACD.
Cho tam giác ABC vuông tại A, . Kẻ đường cao AH.
Chứng minh : từ đó suy ra:
Cho hình bình hành ABCD với đường chéo . Gọi lần lượt là chân đường vuông góc kẻ từ C đến các đường thẳng AB và AD. Gọi G là chân đường vuông góc kẻ từ B đến AC. Chứng minh rằng: tam giác BCG đồng dạng với CAF
Cho hình thang ABCD( AB // CD).
Biết và .
Tính độ dài các cạnh BC và CD.
Qua A vẽ đường thẳng song song với BC, cắt EF ở K. Chứng minh rằng K là trung điểm của EF.
Cho hình thang ABCD( AB // CD).
Biết và .
Chứng minh hai tam giác ADB và BCD đồng dạng.
Cho tam giác có các góc đều nhọn, đường phân giác AD. Các đường cao cắt nhau ở H, đường phân giác AD. Vẽ tia Dx sao cho (tia Dx và A cùng phía đối với BC) tia Dx cắt AC ở K. Chứng minh: tam giác ABE đồng dạng với ACF.Từ đó suy ra: AE.AC = AF. AB.
Cho AD là đường phân giác của tam giác . Vẽ đường thẳng vuông góc với AC tại C cắt đường phân giác AD tại E. Chứng minh tam giác ABD đồng dạng tam giác ECD.