Cho tứ giác ABCD, vẽ các đường thẳng , song song với AC; cắt AD, DC theo thứ tự tại E và F; cắt AB, BC theo thứ tự tại G và H (G, H khác E, F). Chứng minh rằng EG, DB, HF đồng quy.
Giải bởi Vietjack
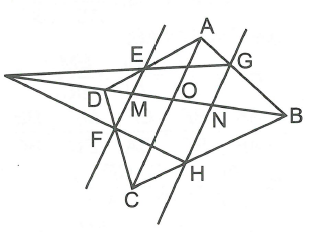
Gọi M, O, N lần lượt là giao điểm của EF, AC, GH với BD.
Vì nên (hệ quả định lý Ta-lét) (1).
Vì nên (hệ quả định lý Ta-lét) (2).
Từ (1) và (2) ta có: (*)
Tương tự có: (**)
Từ (*) và (**) có mà suy ra GE, BD, HF đồng quy. Vậy EG, DB, HF đồng quy.
Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, CA. Chứng minh rằng M, N, P, Q thẳng hàng.
Qua giao điểm O của hai đường chéo tứ giác ABCD, kẻ một đường thẳng tùy ý cắt cạnh AB tại M, CD tại N. Đường thẳng qua M song song với CD cắt AC ở E và đường thẳng qua N song song với AB cắt BD ở F. Chứng minh BE//CF.
