Cho hình thang vuông ABCD () có các điểm E và F thuộc cạnh AD sao cho AE = DF và . Chứng minh
 Giải bởi Vietjack
Giải bởi Vietjack
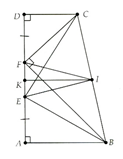
Gọi I, K lần lượt là trung điểm của BC, AD.
Chú ý FEI cân ở I.
Chứng minh: UIE = IB = IC
=> EBC vuông tại E
=>Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB, và K là giao điểm của EM với AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:
a)
Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM.
Cho tam giác ABC. Gọi O là một điểm thuộc miền trong của tam giác. M, N, P, Q lần lượt là trung điểm của các đoạn thẳng OB, OC, AC, AB.
a) Chứng minh tứ giác MNPQ là hình bình hành.
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là hình chữ nhật ?
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật;
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh tứ giác AHCE là hình chữ nhật.