Xác định hàm số $y=ax+b,$  biết đồ thị  (d) của nó đi qua $A\left(2;1,5\right)$  và $B\left(8;-3\right).$  Khi đó hãy tính:

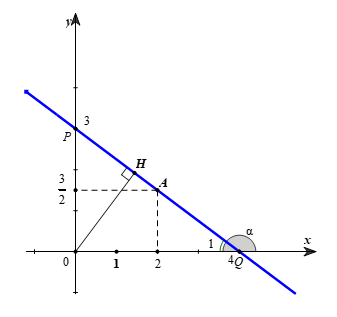
a) Vẽ đồ thị hàm số (d)  vừa tìm được và tính góc $\mathrm{\alpha }$  tạo bởi đường thẳng (d) và trục Ox;

c) Chứng minh rằng khi m thay đổi thì đường thẳng (d) luôn đi qua một điểm cố định.

b) Tìm giá trị của x để hàm số có giá trị bằng  10 , -7

Cho hàm số  $y=(m-3)x+m+2$ (*)

a) Tìm m để đồ thị hàm số (*) cắt trục tung tại điểm có tung độ bằng -3.

c) Chứng minh rằng đồ thị (d) của hàm số  (1) luôn đi qua một điểm cố định với  mọi giá trị của m

Cho hàm số  $y=f\left(x\right)=2x+3$

a) Tính giá trị của hàm số khi  $x=-2; -0,5; 0; 3; \frac{\sqrt{3}}{2}$

b) Xác định m để đồ thị của hàm số song song với nhau.

Viết phương trình đường thẳng (d)   có hệ số góc bằng 7 và đi qua điểm $M\left(2;1\right).$

Cho các hàm số: $y=2mx+m+1 \left(1\right)$  và $y=\left(m-1\right)x+3 \left(2\right)$

a) Xác định m để hàm số (1) đồng biến, còn hàm số (2) nghịch biến.

2) Tìm m để đồ thị hàm số (*)  cắt đồ thị hàm số $y=3x-2$  trong góc phần tư thứ IV

Cho hàm số $y=(2m+1)x+m+4$   (m là tham số) có đồ thị là đường thẳng (d).

a) Tìm m để (d) đi qua điểm $A(-1;2)$ .

Tìm giá trị của tham số  để đường thẳng $d_1:y=-x+2$  cắt đường thẳng $d_2:y=2x+3-k$  tại một điểm nằm trên trục hoành.

c) Tìm m để đồ thị hàm số (*) vuông góc với đường thẳng  y=2x-3

1) Tìm giá trị của m để đồ thị hàm số đi qua:

b, $B\left(\sqrt{2};-5\sqrt{2}\right)$

b) Gọi A , B là giao điểm của đồ thị hàm số (1) với trục tung và trục hoành. Tính diện tích tam giác OAB .