Cho hình thang ABCD, hai đường chéo vuông góc với nhau tại O. Cho biết AD = 12cm; CD = 16cm. Tính các độ dài OA, OB, OC, OD.
 Giải bởi Vietjack
Giải bởi Vietjack
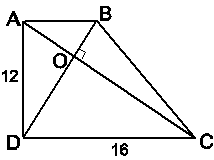
DADC vuông tại D, theo định lí Py-ta-go ta có:
.
Suy ra AC = 20 (cm).
DADC vuông tại D, DO là đường cao nên (hệ thức 3).
Suy ra (cm).
Ta lại có (hệ thức 1) nên (cm).
Do đó (cm).
Xét DABD vuông tại A, AO là đường cao nên (hệ thức 2).
(cm).
Cho tam giác ABC vuông tại A, BC = 20cm. Biết tỉ số hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là 9 : 16. Tính diện tích tam giác ABC.
Cho tam giác ABC cân tại A có các đường cao AH và BK. Chứng minh rằng :
Cho tam giác ABC cân tại A. Các tia phân giác của góc A và góc B cắt nhau tại O. Biết cm, OB = 2cm, tính độ dài AB.
Cho tam giác vuông với các cạnh góc vuông có độ dài là 3 cm và 4 cm , kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng mà nó chia ra trên cạnh huyền.
Cho hình vuông ABCD cạnh 1. Gọi M là một điểm nằm giữa B và C. Tia AM cắt đường thẳng CD tại N. Tính giá trị của biểu thức
Qua O vẽ một đường thẳng song song với hai đáy, cắt AD và BC lần lượt tại M và N. Tính độ dài MN.
Cho tam giác ABC vuông tại A, đường cao AH. Biết diện tích các tam giác ABH và ACH lần lượt là 54cm2 và 96cm2. Tính độ dài BC.