Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi S là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA.
 Giải bởi Vietjack
Giải bởi Vietjack
Trình bày lời giải
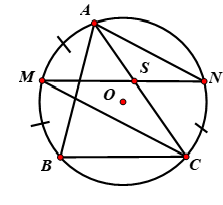
Do M là điểm chính giữa cung nhỏ AB nên sđ sđ
Do MN // BC nên sđ = sđ
Vậy sđ sđ =sđ
(hai góc nội tiếp cùng chắn hai cung bằng nhau)
(hai góc nội tiếp cùng chắn hai cung bằng nhau)
Vậy các tam giác ASN và MSC cân tại C
Nhận xét: Ở bài toán này học sinh có thể nhớ tới bài toán: Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau từ đó nhìn ra
Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác góc A cắt BC tại D và cắt đường tròn tại điểm thứ hai là M. Kẻ tiếp tuyến AK với đường tròn (M, MB), K là tiếp điểm. Chứng minh rằng DK vuông góc với AM.
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Tia phân giác của góc A cắt (O) tại M.
a) CMR : tam giác BMC cân.
Tam giác ABC nội tiếp (O;R). Tia phân giác của góc A cắt (O) tại M. Tia phân giác góc ngoài tại đỉnh A cắt (O) tại N. CMR:
a) Tam giác MBC cân.
Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường kính AM.
a) Tính ;
Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :
a) Tứ giác AMNB là hình thang cân.
Gọi CA, CB lần lượt là các tiếp tuyến của đường tròn (O; R) với A, B là các tiếp điểm. Vẽ đường tròn tâm I qua C và tiếp xúc với AB tại B. Đường tròn (I) cắt đường tròn (O) tại M. Chứng minh rằng đường thẳng AM đi qua trung điểm của BC.
Cho đường tròn tâm O và một dây AB của đường tròn đó. Các tiếp tuyến vẽ từ A và B của đường tròn cắt nhau tại C. Gọi D là một điểm trên đường tròn có đường kính OC ( D khác A và B). CD cắt cung AB của đường tròn (O) tại E. (E nằm giữa C và D). Chứng minh rằng:
a) .
Từ điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB và một cát tuyến MCD. Gọi I là giao điểm của AB và CD. Chứng minh rằng: .
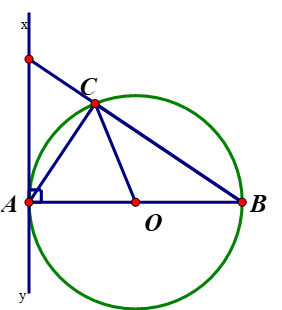
Cho hình vẽ, biết AB là đường kính của đường tròn (O), xy là tiếp tuyến của đường tròn tại A. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
Tam giác ABC nội tiếp đường tròn tâm O. Các điểm M, N, P là điểm chính giữa của các cung AB, BC, CA. Gọi D là giao điểm của MN và AB, E là giao điểm của PN và AC. Chứng minh rằng DE song song với BC.
Trên nửa đường tròn (O) đường kính AB, lấy hai điểm M và N sao cho cung AM = cung MN = cung NB. Gọi P là giao điểm của AM và BN ; H là giao điểm của AN với BM. CMR :
a) Tứ giác AMNB là hình thang cân.
Cho nửa đường tròn (O) đường kính CB, A thuộc nửa đường tròn sao cho AB < AC. Tiếp tuyến tại A cắt đường thẳng BC ở I. Kẻ AH vuông góc với BC. CMR:
a) AB là tia phân giác của góc IAH.
Ghép mỗi ý ở cột bên trái với mỗi ý ở cột bên phải để được khẳng định đúng
|
A. Góc nội tiếp là góc |
1) có số đo bằng 900 |
|
B. Góc nội tiếp chắn nửa đường tròn |
2) bằng nhau. |
|
C. Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì |
3) có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn. |
|
D. Trong một đường tròn, hai góc nội tiếp không bằng nhau, góc lớn hơn thì |
4) chắn dây lớn hơn. |
|
|
5) có cung bị chắn lớn hơn. |
Cho (O) và hai dây AB, CD bằng nhau và cắt nhau tại M. ( C thuộc cung nhỏ AB, B thuộc cung nhỏ CD).
a) CMR: cung AC = cung DB.