Cho tam giác ABC có các góc B và C nhọn, đường cao AH . Dựng ra phía ngoài tam giác ABC các tam giác vuông cân ABD, ACE(). Gọi M là trung điểm của DE. Chứng minh rằng H, A, M thẳng hàng.
Giải bởi Vietjack
Dựng hình bình hành .
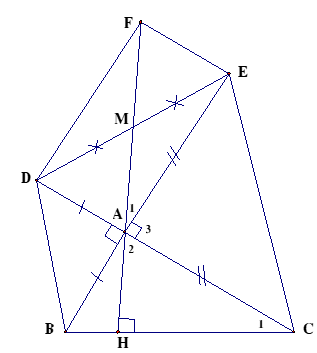
là trung điểm của EF (t/c hình bình hành) và .
Mặt khác (gt); (cùng bù với ).
(c – g – c).
( Hai góc tương ứng).
Mà
.
hay ,A , H thẳng hàng.
Cho tam giác ABC vuông tại A. Đường tròn (O) đường kính AB cắt đường tròn (O’) đường kính AC tại D, M là điểm chính giữa cung nhỏ DC, AM cắt đường tròn (O) tại N, cắt BC tại E. Chứng minh O, N, O’thẳng hàng.
Hai đường tròn và tiếp xúc ngoài tại gọi AC và BC là hai đường kính đi qua C của đường tròn và . DE là dây cung của đường tròn vuông góc với AB tại trung điểm M của AB. Tia DC cắt đường tròn tại điểm thứ 2 là F
a) Tứ giác ADBE là hình gì? Vì sao?
