Cho đoạn thẳng AG và điểm D nằm giữa hai điểm A và G. Trên cùng nửa mặt phẳng bờ AG vẽ các hình vuông ABCD, DEFG. Gọi M, N lần lượt là trung điểm của AG, EC. Gọi I, K lần lượt là tâm đối xứng của các hình vuông ABCD, DEFG.
a) Chứng minh: AE = CG và tại H.
 Giải bởi Vietjack
Giải bởi Vietjack
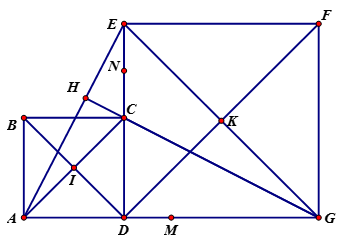
a) Ta có tứ giác là các hình vuông( GT)
Xét và có:
=> AE = CG (Hai cạnh tương ứng) và (Hai góc tương ứng) hay
Ta có: (Hai góc đối đỉnh)
Mà (Hai góc phụ nhau)
Xét có: hay
Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB . Vẽ tại E , tại F . Gọi D là trung điểm của AB . Chứng minh rằng:
a) Tứ giác CFME là hình chữ nhật.
Cho tam giác ABC vuông tại A (AB < AC) , trung tuyến AM . E, F lần lượt là trung điểm của AB, AC.
a) Chứng minh rằng AEMF là hình chữ nhật.
Cho hình chữ nhật ABCD . Tia phân giác góc cắt tia phân giác góc tại M , tia phân giác góc cắt tia phân giác góc tại N . Gọi E, F lần lượt là giao điểm của DM, CN với AB. Chứng minh rằng:
a) AM = DM = BN = CN = ME = NF
Cho hình bình hành ABCD có AB bằng đường chéo AC. Gọi O là trung điểm của BC và E là điểm đối xứng của A qua O. Đường thẳng vuông góc với AE tại E cắt AC tại F .
a) Chứng minh ABEC là hình thoi
Cho tam giác nhọn ABC. Gọi H là trực tâm của tam giác, M là trung điểm của BC. Gọi D là điểm đối xứng của H qua M .
a. Chứng minh tứ giác BHCD là hình bình hành.
Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm của BC, CD. Gọi giao điểm của AM, AN với BD lần lượt là P, Q . Gọi AC cắt BD tại O . Chứng minh rằng:
a)
Cho ABC () có AB < AC. Gọi M là trung điểm của BC . Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E . Vẽ đường cao AH của ABC .
a) Chứng minh ADME là hình chữ nhật.
Cho tam giác ABC vuông tại A , đường trung tuyến AM . Gọi H là điểm đối xứng với M qua AB, E là giao điểm của MH và AB . Gọi K là điểm đối xứng với M qua AC , F là giao điểm của MK và AC .
a) Xác định dạng của tứ giác AEMF, AMBH, AMCK.