30 câu hỏi trắc nghiệm thuộc Dạng 2. Phiếu tự luyện số 2 có đáp án

Câu 1:

Cho tam giác ABC vuông tại A , đường trung tuyến AM . Gọi H là điểm đối xứng với M qua AB, E là giao điểm của MH và AB . Gọi K là điểm đối xứng với M qua AC , F là giao điểm của MK và AC .

a) Xác định dạng của tứ giác AEMF, AMBH, AMCK.

Xem đáp án

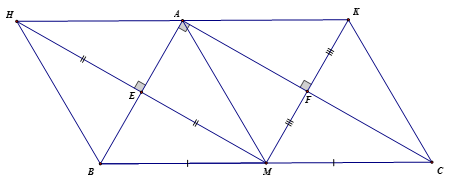
a) Xác định dạng của tứ giác $A E M F, A M B H, A M C K$

H là điểm đối xứng với M qua AB => AB là đường trung trực của HM

$\Rightarrow A H = A M; B H = B M; \hat{A E M} = 90^{°}$

K là điểm đối xứng với M qua AC => AC là đường BM = CM = AM trung trực của KM

$\Rightarrow A M = A K; CM = C K; \hat{A F M} = 90^{°}$

Lại có => AH = BH = BM = AM = MC = CK = AK

Tứ giác AEMF có $\hat{A E M} = \hat{A F M} = \hat{E A F} = 90^{°}$ nên tứ giác AEMF là hình chữ nhật

Tứ giác AMBH có AH = BH = BM = AM nên tứ giác AMBH là hình thoi

Tứ giác AMCK có AM = MC = CK = AK nên tứ giác AMCK là hình thoi

Câu 2:

b) Chứng minh rằng H đối xứng với K qua A .

Xem đáp án

b) Tứ giác AMBH, AMCK là hình thoi => AH // BM; AK // MC mà $M \in B C$ => A, H, K thẳng hàng (theo tiên đề Ơclit)

Lại có AH = AK (cmt) A là trung điểm của HK hay H đối xứng với K qua A

Câu 3:

c) Tam giác vuông ABC có thêm điều kiện gì thì AEMF là hình vuông?

Xem đáp án

c) Hình chữ nhật AEMF là hình vuông <=> EM = AE <=>AB = AC <=>

△

ABC vuông cân tại A .

Câu 4:

Cho tam giác nhọn ABC. Gọi H là trực tâm của tam giác, M là trung điểm của BC. Gọi D là điểm đối xứng của H qua M .

a. Chứng minh tứ giác BHCD là hình bình hành.

Xem đáp án

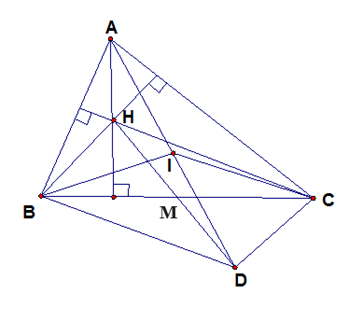
Cho tam giác nhọn ABC. Gọi H là trực tâm của tam giác, M là trung điểm của BC. Gọi D là điểm đối xứng của H qua M . a. Chứng minh tứ giác BHCD là hình bình hành. (ảnh 1)

a. BHCD là hình bình hành:

Vì M vừa là trung điểm của BC vừa là trung điểm của HD nên BHCD là hình bình hành.

Câu 5:

b. Chứng minh các tam giác ABD, ACD vuông tại B, C.

Xem đáp án

b. Tam giác ABD, ACD vuông tại B, C :

BD // CH mà $C H ⊥ A B \Rightarrow B D ⊥ A B$

CD // BH mà $BH ⊥ AC \Rightarrow CD ⊥ AC$

Câu 6:

c. Gọi I là trung điểm của AD . Chứng minh rằng: IA = IB = IC = ID.

Xem đáp án

c. BI, CI l ần lượt là trung tuyến của hai tam giác vuông có chung cạnh huyền AD

=> IA = IB = IC = ID

Câu 7:

Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB . Vẽ $M E ⊥ A C$ tại E , $M F ⊥ B C$ tại F . Gọi D là trung điểm của AB . Chứng minh rằng:

a) Tứ giác CFME là hình chữ nhật.

Xem đáp án

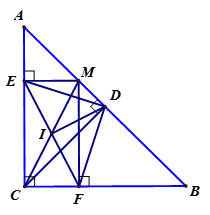
Cho tam giác ABC vuông cân tại C, M là điểm bất kỳ trên cạnh AB . Gọi D là trung điểm của AB . Chứng minh rằng: a) Tứ giác CFME là hình chữ nhật. (ảnh 1)

a) Theo giả thiết thì tứ giác CFME có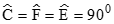

Do đó MECF là hình chữ nhật.

Câu 8:

b) Tam giác DEF vuông cân.

Xem đáp án

b) Gọi I là giao điểm của EF và CM , I là trung điểm của EF và CM .

Vì tam giác ABC vuông cân tại C nên $C D ⊥ A B$ . Xét tam giác DCM vuông tại D, có DI là trung tuyến nên:

$DI = \frac{1}{2} MC = \frac{1}{2} EF$ . Mà DI cũng là trung tuyến trong tam giác DEF , do vậy tam giác DEF vuông tại D.

Trong tứ giác CEDF có $\hat{CED} + \hat{CFD} = 180^{°} \Rightarrow \hat{CED} = \hat{BFD}$ (1).

Dễ thấy 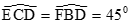(2) và $E C = M F = B F$ (3) (tam giác BFM vuông cân tại ).

Từ (1), (2), (3) suy ra hai tam giác CED và CFD bằng nhau (g-c-g).

Từ đó DE = DF . Vậy tam giác DEF vuông cân tại .

Câu 9:

Cho tam giác ABC vuông tại A (AB < AC) , trung tuyến AM . E, F lần lượt là trung điểm của AB, AC.

a) Chứng minh rằng AEMF là hình chữ nhật.

Xem đáp án

Cho tam giác ABC vuông tại A (AB < AC) , trung tuyến AM . E, F lần lượt là trung điểm của AB, AC. a) Chứng minh rằng AEMF là hình chữ nhật. (ảnh 1)

a) Theo tính chất tam giác vuông, ta có AM = MC = MB.

Tam giác CMA cân tại A và F là trung điểm AC suy ra $M F ⊥ A C$ .

Chứng minh tương tự: $M E ⊥ A B$ .

Vậy AEMF là hình chữ nhật.

Câu 10:

b) Gọi AH là đường cao của tam giác ABC. Chứng minh EHMF là hình thang cân

Xem đáp án

b) Ta có EF là đường trung bình trong tam giác ABC, suy ra . Theo giả thiết, AB < AC suy ra HB < HA , do đó H thuộc đoạn MB . Vậy EHMF là hình thang. (1)

Tam giác HAB vuông tại H, ta có HE = EA = EB, từ đó suy ra $Δ A H E$ cân tại E

Ta có: $\{\begin{cases} E F / / B C \\ A H ⊥ B C \end{cases} \Rightarrow E F ⊥ A H$ suy ra $Δ A H E$ cân tại E có EF là đường cao đồng thời là đường phân giác $\Rightarrow \hat{A E F} = \hat{H E F}$

mà $\hat{A E F} = \hat{M F E}$ . Do đó $\Rightarrow \hat{M E F} = \hat{H E F}$ (2)

Từ (1) và (2) suy ra: EHMF là hình thang cân.

Câu 11:

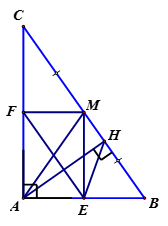
Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm của BC, CD. Gọi giao điểm của AM, AN với BD lần lượt là P, Q . Gọi AC cắt BD tại O . Chứng minh rằng:

a) $A P = \frac{2}{3} A M, A Q = \frac{2}{3} A N$

Xem đáp án

Cho hình chữ nhật ABCD. Gọi M, N lần lượt là trung điểm của BC, CD. Gọi AC cắt BD tại O . Chứng minh rằng: a) AP = 2/3AM, AQ = 2/3AN (ảnh 1)

a) Ta có O là trung điểm của AC và BD .

Trong tam giác ABC, AM và BO là hai đường trung tuyến, do đó P là trọng tâm tam giác ABC. Từ đó ta có $A P = \frac{2}{3} A M$ .

Chứng minh tương tự, ta có $A Q = \frac{2}{3} A N$

Câu 12:

b) BP = PQ = QD = 2OP.

Xem đáp án

b) Ta có: $B P = \frac{2}{3} B O = \frac{1}{3} B D$ ; tương tự, $D Q = \frac{1}{3} B D$ , suy ra $P Q = \frac{1}{3} B D$ .

Mặt khác $O P = O Q = \frac{1}{3} O B$ , do đó O là trung điểm PQ.

Vậy BP = PQ = QD = 2OP.

Câu 13:

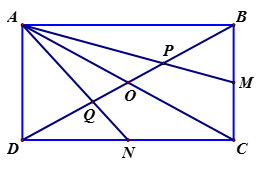
Cho tứ giác ABCD có ABCD . Gọi M, N, P, Q lần lượt là trung điểm của BC, BD, AD, AC. Chứng minh rằng:

a) Tứ giác MNPQ là hình chữ nhật.

Xem đáp án

Cho tứ giác ABCD có ABCD . Gọi M, N, P, Q lần lượt là trung điểm của BC, BD, AD, AC. Chứng minh rằng: a) Tứ giác MNPQ là hình chữ nhật. (ảnh 1)

a) Trong tam giác ACD, PQ là đường trung bình, suy ra PQ // CD

Tương tự $M N / / C D, M Q / / A B, N P / / A B$ .

Từ đó ta có MN // PQ và NP // MQ

Suy ra MNPQ là hình bình hành.

Mặt khác, $A B ⊥ C D \Rightarrow M N ⊥ M Q$ .

Vậy MNPQ là hình chữ nhật.

Câu 14:

b) Biết BC // AD, BC = 4cm, AD = 16cm. Tính MP

Xem đáp án

b) Ta có MP = NQ. Theo giả thiết thì BCAD là hình thang với hai đáy BC, AD có QN là đường trung bình nên $M P = N Q = \frac{1}{2} (B C + A D) = 10 c m$ .

Câu 15:

Cho hình chữ nhật ABCD . Tia phân giác góc $\hat{A}$ cắt tia phân giác góc $\hat{D}$ tại M , tia phân giác góc $\hat{B}$ cắt tia phân giác góc $\hat{C}$ tại N . Gọi E, F lần lượt là giao điểm của DM, CN với AB. Chứng minh rằng:

a) AM = DM = BN = CN = ME = NF

Xem đáp án

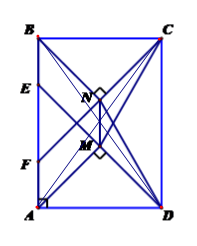
Cho hình chữ nhật ABCD . Tia phân giác góc A cắt tia phân giác góc D tại M Chứng minh rằng: a) AM = DM = BN = CN = ME = NF (ảnh 1)

a) Dễ thấy các tam giác $A D M, B C N, A M E, B N F$ là các tam giác vuông cân với các đỉnh lần lượt là $M, N, M, N$ .

do đó $A M = D M = E M$ và $B N = C N = F N$ .

Mặt khác, vì AD = BC nên .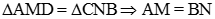

Vậy $A M = D M = E M = B N = C N = F N$ .

Câu 16:

b) Tứ giác DMNC là hình thang cân.

Xem đáp án

b) Tam giác ADE vuông tại A có 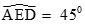$\hat{A D E} = 45^{0}$ => . Lại có 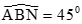, do đó BN // EM .

Theo trên BN = EM, do vậy BNME là hình bình hành, suy ra MN // BE // CD.

Suy ra CDMN là hình thang, mà $\hat{D C N} = \hat{C D M} (= 45^{0})$

Vậy CDMN là hình thang cân.

Câu 17:

c) AF = BE

Xem đáp án

c) Chứng minh tương tự như trên, ta có ÀNM cũng là hình bình hành.

Từ đó suy ra AF = BE = MN.

Câu 18:

c) AC, BD, MN đồng quy

Xem đáp án

d) Theo chứng minh trên ta có BN // MD và BN = MD, do đó BNDM là hình bình hành, suy ra BD và MN cắt nhau tại trung điểm mỗi đoạn. Mặt khác BD và AC cũng cắt nhau tại trung điểm mỗi đoạn.

Vậy AC, BD, MN đồng quy tại trung điểm mỗi đoạn.

Câu 19:

Cho $△$ ABC ( $\hat{A} = 90^{0}$ ) có AB < AC. Gọi M là trung điểm của BC . Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E . Vẽ đường cao AH của $△$ ABC .

a) Chứng minh ADME là hình chữ nhật.

Xem đáp án

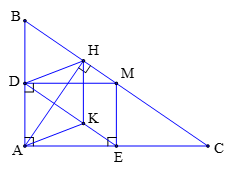
Cho ABC (góc A = 90 độ) có AB < AC. Gọi M là trung điểm của BC . a) Chứng minh ADME là hình chữ nhật. (ảnh 1)

a) Tứ giác ADME có:

$\hat{A} = \hat{D} = \hat{E} = 90 °$ nên ADME là hình chữ nhật.

Câu 20:

b) Chứng minh CMDE là hình bình hành.

Xem đáp án

b) $M D ⊥ A B, A C ⊥ A B$ , suy ra MD // AC .

Vì M là trung điểm của BC nên MD là đường trung bình của $△$ ABC .

Tương tự, ME cũng là đường trung bình của $△$ ABC . Từ đó ta có D, E lần lượt là trung điểm của AB, AC .

Suy ra MD // CE và DE // MC. Vậy CMDE là hình bình hành.

Câu 21:

c) Chứng minh MHDE là hình thang cân.

Xem đáp án

c) Theo trên thì DE // HM (1).

Xét tam giác ACH vuông tại H , có HE là trung tuyến nên $H E = \frac{1}{2} A C \Rightarrow H E = A E$ .

Mặt khác, ADME là hình chữ nhật (cmt) nên $A E = D M$

Suy ra HE = DM (2).

Từ (1) và (2) suy ra MHDE là hình thang cân.

Câu 22:

d) Qua A kẻ đường thẳng song song với DH cắt DE tại K . Chứng minh

H K ⊥ A C

.

Xem đáp án

d) Xét hai tam giác ADK và DBH , có:

$D E / / B C \Rightarrow \hat{A D K} = \hat{D B H}$ (Hai góc đồng vị).

AD = DB (vì D là trung điểm của AB)

DH // AK $\Rightarrow \hat{D A K} = \hat{B D H}$ (Hai góc đồng vị).

Suy ra $Δ A D K = Δ D B H$ => AK = DH .

Lại có AK // DH, do đó ADHK là hình bình hành, suy ra HK // DA .

Vì $D A ⊥ A C$ nên $H K ⊥ A C$ .

Câu 23:

Cho hình bình hành ABCD có AB bằng đường chéo AC. Gọi O là trung điểm của BC và E là điểm đối xứng của A qua O. Đường thẳng vuông góc với AE tại E cắt AC tại F .

a) Chứng minh ABEC là hình thoi

Xem đáp án

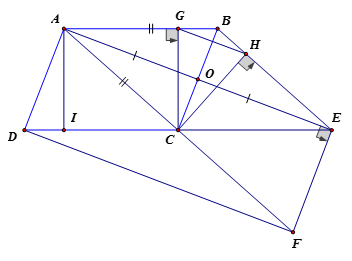
Cho hình bình hành ABCD có AB bằng đường chéo AC. Gọi O là trung điểm của BC . a) Chứng minh ABEC là hình thoi (ảnh 1)

a) Vì E đối xứng với A qua O nên O là trung điểm AE mà O cũng là trung điểm BC nên tứ giác ABEC là hình bình hành mà AB = AC (gt)

Vậy tứ giác ABEC là hình thoi.

Câu 24:

b) Chứng minh tứ giác ADFE là hình chữ nhật

Xem đáp án

b) Tứ giác ABC là hình bình hành nên AB // CD và AB = CD

Tứ giác ABEC là hình thoi nên

AB // CE và AB = CE

=> C, D, E thẳng hàng và CD = CE

=> C là trung điểm của DE (1)

Xét tam giác AEF vuông tại E có: AC = CE (vì ABEC là hình thoi) nên tam giác ACE cân.

$\hat{C A E} = \hat{C E A}$ , lại có $\hat{C F E} + \hat{C A E} = \hat{C E F} + \hat{C E A} = 90^{o}$

Vậy $\hat{C E F} = \hat{C F E}$ hay tam giác CEF cân tại C suy ra CE = CF = AC.

=> C là trung điểm AF (2)

Từ (1) và (2) ta có: AEFD là hình bình hành

Mà AE $⊥$ EF nên AEFD là hình chữ nhật.

Câu 25:

c) Vẽ

C G ⊥ A B

tại

G, C H ⊥ B E

tại H . Chứng minh GH // AE .

Xem đáp án

c) Xét $Δ B G C$ và $Δ B H C$ có:

BC là cạnh chung

$\hat{B G C} = \hat{B H C} = 90^{o}$

$\hat{G B C} = \hat{H B C}$ (vì BC là p/g góc ABE của hình thoi ABEC)

Vậy $Δ B G C = Δ B H C$ (cạnh huyền, góc nhọn)

=> BG = BH mà BA = BE

$\begin{array}{l} \Rightarrow \frac{B G}{B A} = \frac{B H}{B E} \\ \Rightarrow GH / / AE \end{array}$

Câu 26:

d) Vẽ

A I ⊥ C D

tại I . Chứng minh rằng nếu AI = AO thì

A C ⊥ B D

và

\hat{A B O} = 60 °

Xem đáp án

d) Xét $Δ A C I$ và $Δ A C O$ có:

AC chung

$\hat{A I C} = \hat{A O C} = 90^{o}$

AI = AO

Vậy $Δ A C I = Δ A C O$ (cạnh huyền – cạnh góc vuông)

=> $\hat{A C I} = \hat{A C O}$ (2 góc tương ứng)

=> AC là tia phân giác góc BCD

=> Hình bình hành ABCD là hình thoi

$\Rightarrow A C ⊥ B D$ (đpcm) và BC = CD => BC = AB

Mà AB = AC (do ABCE là hình thoi)

$\Rightarrow Δ A B C$ đều => $\hat{A B O} = 60 °$ (đpcm)

Câu 27:

Cho đoạn thẳng AG và điểm D nằm giữa hai điểm A và G. Trên cùng nửa mặt phẳng bờ AG vẽ các hình vuông ABCD, DEFG. Gọi M, N lần lượt là trung điểm của AG, EC. Gọi I, K lần lượt là tâm đối xứng của các hình vuông ABCD, DEFG.

a) Chứng minh: AE = CG và $A E ⊥ C G$ tại H.

Xem đáp án

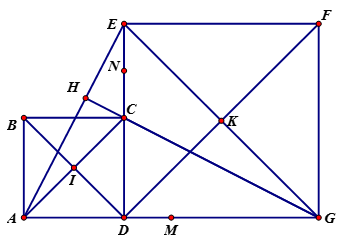
Cho đoạn thẳng AG và điểm D nằm giữa hai điểm A và G. a) Chứng minh: AE = CG và AE vuông góc CG tại H. (ảnh 1)

a) Ta có tứ giác $A B C D, D E F G$ là các hình vuông( GT)

$\Rightarrow \{\begin{cases} A B = B C = C D = A D; \hat{A} = \hat{B} = \hat{C} = \hat{D} \\ D E = E F = F G = D G; \hat{D} = \hat{E} = \hat{F} = \hat{G} \end{cases}$

Xét và có:

$\begin{array}{l} A D = C D (c m t) \\ \hat{A D E} = \hat{C D G} = 90 ° \\ E D = D G (c m t) \end{array}\} \Rightarrow Δ A D E = Δ C D G (c . g . c)$

=> AE = CG (Hai cạnh tương ứng) và $\hat{A E D} = \hat{C G D}$ (Hai góc tương ứng) hay $\hat{H E C} = \hat{C G D}$

Ta có: $\hat{H C E} = \hat{D C G}$ (Hai góc đối đỉnh)

Mà $\hat{C G D} + \hat{D C G} = 90 °$ (Hai góc phụ nhau)

$\Rightarrow \hat{H C E} + \hat{H E C} = 90 °$

Xét $△ H E C$ có: $\hat{H C E} + \hat{H E C} = 90^{°} (c m t) \Rightarrow \hat{E H C} = 90^{°}$ hay $A E ⊥ C G = {H}$

Câu 28:

b) Chứng minh IMKN là hình vuông.

Xem đáp án

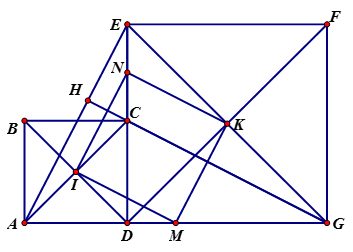
b) Chứng minh IMKN là hình vuông. (ảnh 1)

b) Xét $△$ AEC có: I là trung điểm của AC, N là trung điểm của EC

=> IN là đường trung bình của $△$ AEC

$\Rightarrow IN / / AE; IN = \frac{AE}{2}$

Xét $△$ AEG có: K là trung điểm của EG, M là trung điểm của AG

=> KM là đường trung bình của $△ A E G$ (ĐN)

$\Rightarrow K M / / A E; K M = \frac{A E}{2}$

Xét tứ giác MINK có:

$\begin{array}{l} IN = KM (= \frac{AE}{2}) \\ IN / / KM (/ / AE) \end{array}\} \Rightarrow$ Tứ giác MINK là hình bình hành (dhnb)

Tương tự ta cũng chứng minh được IM là đường trung bình của $△$ ACG

=> IM // CG; IM = $\frac{C G}{2}$ mà KM = $\frac{A E}{2}$ và AE = CG (cmt)

=> IM = KM mà tứ giác MINK là hình bình hành

Do đó tứ giác MINK là hình thoi.

Ta có 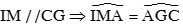( Hai góc đồng vị)

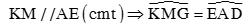b) Chứng minh IMKN là hình vuông. (ảnh 3)

( Hai góc đồng vị)

Mà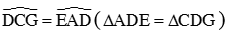

Nên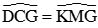

Mà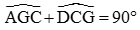

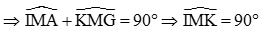
b) Chứng minh IMKN là hình vuông. (ảnh 7)

Mà tứ giác MINK là hình thoi (cmt)

Vậy tứ giác MINK là hình vuông (đpcm)

Câu 29:

c) Chứng minh B, H , F thẳng hàng.

Xem đáp án

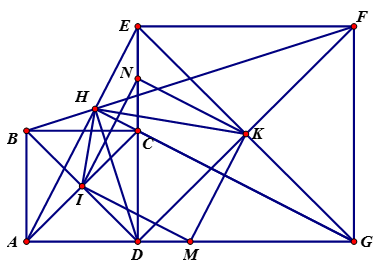
c) Chứng minh B, H , F thẳng hàng. (ảnh 1)

Nối IH, HK

Ta có $AE ⊥ CG = {H} (CMT) \Rightarrow \hat{EHG} = \hat{AHC} = 90^{°}$

Xét $△$ EHG có: 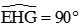và K là trung điểm của EG (Tứ giác DEFG là hình vuông)

Do đó HK là đường trung tuyến ứng với cạnh huyền EG

=> HK = $\frac{E G}{2}$ (TC) mà EG = DF ( Tứ giác DEFG là hình vuông)

=> HK = $\frac{D F}{2}$

Xét $△$ DHF có: HK = $\frac{D F}{2}$ => $△$ DHF vuông tại D =>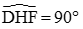

Tương tự ta cũng chứng minh được: IH = $\frac{A C}{2}$ mà AC = BD => IH = $\frac{B D}{2}$

=> Tam giác BHD vuông tại H(TC)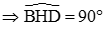

Do đó: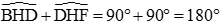

Vậy B, H , F thẳng hàng.

Câu 30:

d) Gọi T là giao điểm của BF và EG . Chứng minh rằng độ dài TN không đổi khi di D động trên đoạn AG cố định.

Xem đáp án

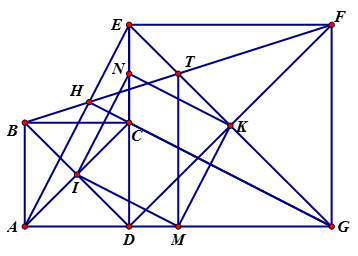
d) Gọi T là giao điểm của BF và EG . Chứng minh rằng độ dài TN không đổi khi di D động trên đoạn AG cố định. (ảnh 1)

Ta có tứ giác ABCD, DEFG là hình vuông (gt)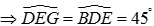

Mà hai góc này ở vị trí so le trong => EG // BD

Xét: $△$ BDF có K là trung điểm của DF mà EG // BD (cmt) hay TK // BD

=> T là trung điểm của BF

Ta có :

$\begin{array}{l} \hat{B A D} = \hat{F G D} = 90^{°} \\ \Rightarrow A B ⊥ A G; F G ⊥ A G \\ \Rightarrow A B / / F G \end{array}$

=> Tứ giác ABFG là hình thang

Ta có: T là trung điểm của BF (cmt), M là trung điểm của AG (gt)

=> TM là đường trung bình của hình thang ABFG

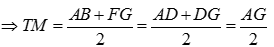
d) Gọi T là giao điểm của BF và EG . Chứng minh rằng độ dài TN không đổi khi di D động trên đoạn AG cố định. (ảnh 3)

Mà AG không đổi nên độ dài TM không đổi khi D di động trên đoạn AG cố định.