Cho ∆ABC cân tại B có chu vi là 60cm, đường cao BH. Biết chu vi ∆ABH là 40cm. Độ dài BH là
A. 10 cm;
B. 20 cm;
C. 25 cm;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
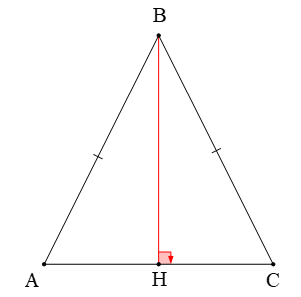
∆ABC cân tại B ⇒ BA = BC và (tính chất tam giác cân)
Xét hai tam giác vuông BAH và BCH có
BA = BC
Suy ra ∆BAH = ∆BCH (cạnh huyền – góc nhọn)
Do đó AH = CH (hai cạnh tương ứng)
Mà chu vi ∆ABC = BA + BC + AC
⇒ chu vi ∆ABC = 2BA + 2AH
⇒ 2(BA + AH) = 60
⇒ BA + AH = 30 (cm)
Ta có: chu vi ∆BAH = BA + AH + BH
⇒ 30 + BH = 40
⇒ BH = 10 (cm).
Cho tam giác nhọn MNP có hai đường cao NE và PF cắt nhau tại H. Biết NE = PF. Khẳng định đúng là
Cho ∆ABC có diện tích là 180 cm2 và cạnh BC = 20 cm. Độ dài đường cao ứng với cạnh BC là
Cho ∆ABC cân tại A có trực tâm I. Biết . Số đo các góc của ∆ABC là
Cho ∆ABC nhọn, hai đường cao BD và CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. So sánh đúng là
