7 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 CD Bài 13. Tính chất ba đường cao của tam giác (Thông hiểu) có đáp án

Trắc nghiệm Toán 7 CD Bài 13. Tính chất ba đường cao của tam giác (Phần 2) có đáp án

Trắc nghiệm Toán 7 CD Bài 13. Tính chất ba đường cao của tam giác (Thông hiểu) có đáp án

1128 lượt thi
7 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho tam giác ABC cân tại B có đường cao BH. Khẳng định đúng là

A. BH là đường trung tuyến của ∆ABC;

B. BH là đường phân giác của ∆ABC;

C. BH là đường trung trực của ∆ABC;

D. Cả A, B và C đều đúng.

Xem đáp án

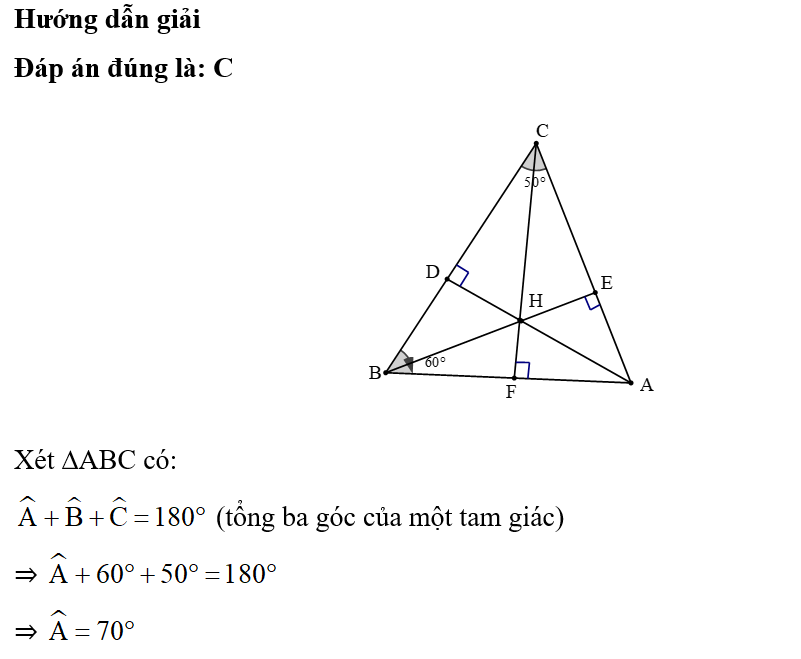
Hướng dẫn giải

Đáp án đúng là: D

Xét hai tam giác vuông ABH và CBH có

BA = BC (tam giác BAC cân tại B)

$\hat{A} = \hat{C}$ (tính chất tam giác cân)

Suy ra ∆ABH = ∆CBH (cạnh huyền – góc nhọn)

Do đó AH = CH (hai cạnh tương ứng) ⇒ H là trung điểm của AC ⇒ BH là đường trung tuyến của ∆ABC.

Mà BH ⊥ AC nên BH là đường trung trực của ∆ABC.

$\hat{A B H} = \hat{C B H}$ (hai góc tương ứng) ⇒ BH là tia phân giác góc ABC hay BH là đường phân giác của của ∆ABC.

Câu 2:

Cho ∆ABC có $\hat{B} = 60 °; \hat{C} = 50 °$ . Ba đường cao AD, BE, CF cắt nhau tại H. Số đo $\hat{B H C}$ là

A. 98°;

B. 108°;

C. 110°;

D. 70°.

Xem đáp án

Cho tam giác ABC có góc B=60 độ, góc C=50 độ. Ba đường cao AD, BE, CF cắt nhau tại H. (ảnh 1)

Cho tam giác ABC có góc B=60 độ, góc C=50 độ. Ba đường cao AD, BE, CF cắt nhau tại H. (ảnh 2)

Câu 3:

Cho tam giác nhọn MNP có hai đường cao NE và PF cắt nhau tại H. Biết NE = PF. Khẳng định đúng là

A. ∆MNP cân tại N;

B. ∆MEF cân tại E;

C. H là trọng tâm ∆MNP;

D. MH ⊥ BC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

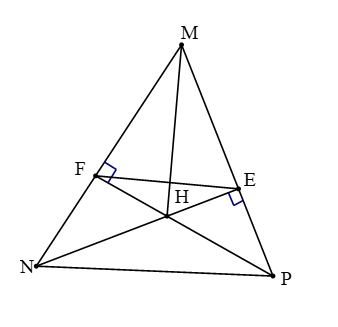
∆MNP có hai đường cao NE và PF cắt nhau tại H

⇒ H là trực tâm ∆MNP

⇒ MH ⊥ BC

Xét ∆MNE và ∆MPF có

$\hat{M E N} = \hat{M F P} = 90 °$

NE = PF (giả thiết)

$\hat{M N E} = \hat{M P F}$ (cùng phụ góc M)

Suy ra ∆MNE = ∆MPF (g.c.g)

Do đó MN = MP (hai cạnh tương ứng) ⇒ ∆MNP cân tại M

ME = MF (hai cạnh tương ứng) ⇒ ∆MFE cân tại M.

Câu 4:

Cho ∆ABC cân tại B có chu vi là 60cm, đường cao BH. Biết chu vi ∆ABH là 40cm. Độ dài BH là

A. 10 cm;

B. 20 cm;

C. 25 cm;

D. 30 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

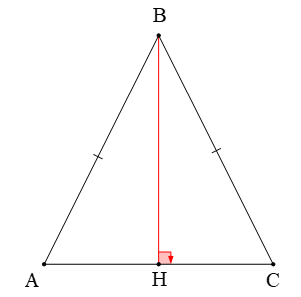
Cho tam giác ABC cân tại B có chu vi là 60cm, đường cao BH. Biết chu vi tam giác ABH là 40cm. (ảnh 1)

∆ABC cân tại B ⇒ BA = BC và $\hat{A} = \hat{C}$ (tính chất tam giác cân)

Xét hai tam giác vuông BAH và BCH có

BA = BC

$\hat{A} = \hat{C}$

Suy ra ∆BAH = ∆BCH (cạnh huyền – góc nhọn)

Do đó AH = CH (hai cạnh tương ứng)

Mà chu vi ∆ABC = BA + BC + AC

⇒ chu vi ∆ABC = 2BA + 2AH

⇒ 2(BA + AH) = 60

⇒ BA + AH = 30 (cm)

Ta có: chu vi ∆BAH = BA + AH + BH

⇒ 30 + BH = 40

⇒ BH = 10 (cm).

Câu 5:

Cho ∆ABC có diện tích là 180 cm² và cạnh BC = 20 cm. Độ dài đường cao ứng với cạnh BC là

A. 9 cm;

B. 18 cm;

C. 4,5 cm;

D. 20 cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

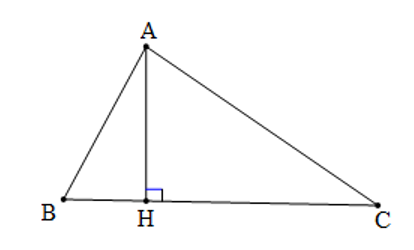
Cho tam giác ABC có diện tích là 180 cm^2 và cạnh BC = 20 cm. Độ dài đường cao ứng với cạnh BC là (ảnh 1)

Kẻ AH ⊥ BC tại H. Khi đó AH là đường cao ứng với cạnh BC

⇒ S_ABC = $\frac{1}{2} A H . B C$

⇒ $\frac{1}{2} A H .20 = 180$

⇒ AH = 18 (cm)

Vậy AH = 18 cm.

Câu 6:

Cho ∆ABC cân tại A có trực tâm I. Biết $\hat{B I C} = 120 °$ . Số đo các góc của ∆ABC là

A. $\hat{A} = 120 °$ ; $\hat{B} = \hat{C} = 30 °$ ;

B. $\hat{A} = 80 °$ ; $\hat{B} = \hat{C} = 50 °$ ;

C. $\hat{A} = \hat{B} = \hat{C} = 60 °$ ;

D. Không đủ dữ kiện để xác định.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Gọi BI cắt AC tại H, CI cắt AB tại K

⇒ BH, CK là đường cao của ∆ABC

Ta có $\hat{B I C} + \hat{C I H} = 180 °$ (hai góc kề bù)

⇒ $120 ° + \hat{C I H} = 180 °$

⇒ $\hat{C I H} = 60 °$

∆CIH vuông tại H ⇒ $\hat{C I H} + \hat{H C I} = 90 °$

∆CKA vuông tại K ⇒ $\hat{B A C} + \hat{H C I} = 90 °$

Do đó $\hat{B A C} = \hat{C I H}$

⇒ $\hat{B A C} = 60 °$

Mà ∆ABC cân (giả thiết)

Suy ra ∆ABC đều

Do đó $\hat{A} = \hat{B} = \hat{C} = 60 °$ .

Câu 7:

Cho ∆ABC nhọn, hai đường cao BD và CE gặp nhau tại H. Vẽ điểm K sao cho AB là trung trực của HK. So sánh đúng là

A. $\hat{K A B} = \hat{K C B}$ ;

B. $\hat{K A B} > \hat{K C B}$ ;

C. $\hat{K A B} < \hat{K C B}$ ;

D. Không đủ dữ kiện để so sánh.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

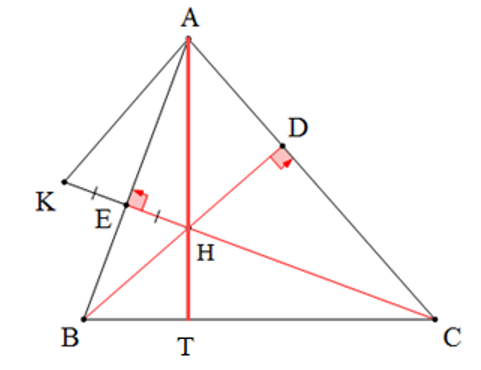
Cho tam giác ABC nhọn, hai đường cao BD và CE gặp nhau tại H. Vẽ điểm K sao cho AB (ảnh 1)

Gọi AH cắt BC tại T ⇒ AT là đường cao của ∆ABC.

Có AB là trung trực của HK (giả thiết) ⇒ KE = HE và AE ⊥ KH

Xét ∆AKE và ∆AHE có

AE là cạnh chung

$\hat{A E K} = \hat{A E H} = 90 °$

KE = HE

Suy ra ∆AKE = ∆AHE (c.g.c)

Do đó $\hat{K A E} = \hat{H A E}$ (hai góc tương ứng)

Hay $\hat{K A B} = \hat{T A B}$ (1)

∆TAB vuông tại T ⇒ $\hat{T A B} + \hat{A B C} = 90 °$

∆ECB vuông tại E ⇒ $\hat{E C B} + \hat{A B C} = 90 °$

Do đó $\hat{T A B} = \hat{E C B}$ hay $\hat{T A B} = \hat{K C B}$ (2)

Từ (1) và (2) suy ra $\hat{K A B} = \hat{K C B}$ .

Bắt đầu thi ngay