Cho hình chóp S.ABCD có đáy là hình bình hành với AB = a, AD = 2a .
Tam giác SAB vuông cân tại A ,M M là một điểm trên cạnh AD ( M khác A và D ). Mặt phẳng đi qua và song song với (SAB) cắt BC, SC, SD lần lượt tại N, P, Q .
a) MNPQ là hình gi?.
 Giải bởi Vietjack
Giải bởi Vietjack
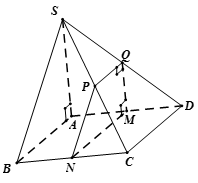
a) Ta có
Tương tự
Dễ thấy nên MNPQ là hình bình hành
Lại có
Vậy MNPQ là hình thang vuông.
Cho tứ diện đều ABCD có cạnh bằng a . Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, AD, BC và AC .
a) Khẳng định nào sau đây là đúng nhất?
Cho tứ diện ABCD có AB vuông góc với CD, AB = 4, CD = 6. M là điểm thuộc cạnh BC sao cho MC = 2BM. Mặt phẳng (P) đi qua M song song với AB và CD. Diện tích thiết diện của (P) với tứ diện là?
Cho hình lập phương ABCD.A'B'C'D' cạnh a . Trên các cạnh DC và BB' lấy các điểm M và N sao cho .
a) Khẳng định nào sau đây là đúng?
Cho tứ diện ABCD . Chứng minh rằng nếu thì . Điều ngược lại đúng không?
Sau đây là lời giải:
Bước 1:
Bước 2: Chứng minh tương tự, từ AC.AD = AD.AB ta được và AB.AC = AD.AB ta được .
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?