A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
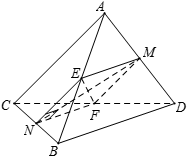
Gọi E, F lần lượt là trung điểm của AB và CD .
Ta có: (1).
Mà: (2).
Từ (1), (2) => MENF là hình chữ nhật.
Từ đó ta có:
Cho hình chóp S.ABCD có đáy là hình bình hành với AB = a, AD = 2a .
Tam giác SAB vuông cân tại A ,M M là một điểm trên cạnh AD ( M khác A và D ). Mặt phẳng đi qua và song song với (SAB) cắt BC, SC, SD lần lượt tại N, P, Q .
a) MNPQ là hình gi?.
Cho tứ diện đều ABCD có cạnh bằng a . Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, AD, BC và AC .
a) Khẳng định nào sau đây là đúng nhất?
Cho tứ diện ABCD có AB vuông góc với CD, AB = 4, CD = 6. M là điểm thuộc cạnh BC sao cho MC = 2BM. Mặt phẳng (P) đi qua M song song với AB và CD. Diện tích thiết diện của (P) với tứ diện là?
Cho hình lập phương ABCD.A'B'C'D' cạnh a . Trên các cạnh DC và BB' lấy các điểm M và N sao cho .
a) Khẳng định nào sau đây là đúng?
Cho tứ diện ABCD . Chứng minh rằng nếu thì . Điều ngược lại đúng không?
Sau đây là lời giải:
Bước 1:
Bước 2: Chứng minh tương tự, từ AC.AD = AD.AB ta được và AB.AC = AD.AB ta được .
Bước 3: Ngược lại đúng, vì quá trình chứng minh ở bước 1 và 2 là quá trình biến đổi tương đương.
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?