A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D.
(Hình vẽ của câu 19)
Hai tam giác vuông SBC và SDC nên có chung chân đường cao M kẻ từ B và D
. Ta đi tính góc
Trong tam giác vuông SBC ta có:
. Tương tự
Áp dụng định lý cosin cho ta có:
Hay
Trong không gian cho tam giác ABC. Tìm điểm M sao cho giá trị của biểu thức 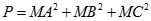 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và 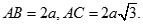 Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30o. Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC)
Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30o. Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC)
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và 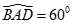 . Gọi O, O' lần lượt là tâm của hai đáy, gọi S là trung điểm của OO'. Tính khoảng cách từ O tới mặt phẳng (SAB) biết OO' = 2a
. Gọi O, O' lần lượt là tâm của hai đáy, gọi S là trung điểm của OO'. Tính khoảng cách từ O tới mặt phẳng (SAB) biết OO' = 2a
Cho hình chóp đều S.ABC có cạnh đáy bằng a. Gọi O là tâm của đáy và 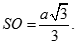 Tính khoảng cách từ O tới SA
Tính khoảng cách từ O tới SA