Cho hình chóp S.ABC có SA = SB = SC, , . Vẽ 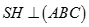 ,
, 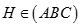 . Khẳng định nào sau đây đúng:
. Khẳng định nào sau đây đúng:
A. H trùng với trung điểm của AB
C. H trùng với trung điểm của BC
D. H trùng với trung điểm của AC
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D.
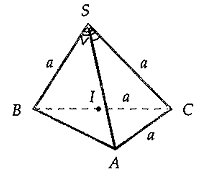
Gọi SA = SB = SC = a
Ta có: tam giác SAC đều => AC = SA = a.
Tam giác SAB vuông cân tại 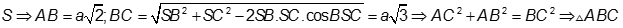
vuông tại A . Gọi I là trung điểm của BC thì I là tâm đường tròn ngoại tiếp tam giác ABC. Gọi d là trục của tam giác ABC thì d đi qua I và 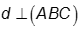
Mặt khác: SA = SB = SC nên 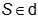 .
.
Vậy 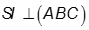 nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC).
nên I là hình chiếu vuông góc của S lên mặt phẳng (ABC).
Trong không gian cho tam giác ABC. Tìm điểm M sao cho giá trị của biểu thức 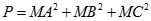 đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và 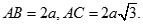 Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30o. Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC)
Hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm H của cạnh AB. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng 30o. Tính khoảng cách từ trung điểm M của cạnh BC đến mặt phẳng (SAC)
Cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và 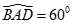 . Gọi O, O' lần lượt là tâm của hai đáy, gọi S là trung điểm của OO'. Tính khoảng cách từ O tới mặt phẳng (SAB) biết OO' = 2a
. Gọi O, O' lần lượt là tâm của hai đáy, gọi S là trung điểm của OO'. Tính khoảng cách từ O tới mặt phẳng (SAB) biết OO' = 2a
Cho hình chóp đều S.ABC có cạnh đáy bằng a. Gọi O là tâm của đáy và 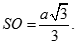 Tính khoảng cách từ O tới SA
Tính khoảng cách từ O tới SA