Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, CD, SA (Tham khảo hình vẽ). Có bao nhiêu khẳng định đúng trong các khẳng định sau
i) \(\left( {MNP} \right)||\left( {SBC} \right)\). ii) \(NP||\left( {SBC} \right)\). 3i) \(MP||\left( {SCD} \right)\). 4i) \(MP||\left( {SBC} \right)\).
Giải bởi Vietjack
Đáp án C
Phương pháp:
Dựa vào tính chất song song để chứng minh.
Cách giải:
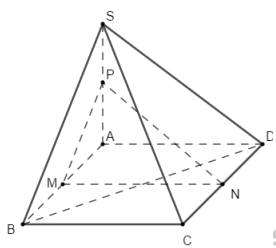
Ta có M, N, P lần lượt là trung điểm của AB, CD, SA.
Nên ta có \(\left\{ \begin{array}{l}MN||BC\\MP||SB\end{array} \right. \Rightarrow \left( {MNP} \right)||\left( {SBC} \right) \Rightarrow \left\{ \begin{array}{l}NP||\left( {SBC} \right)\\MP||\left( {SBC} \right)\end{array} \right.\)
Ta có \(MP||SB\); SB cắt \(\left( {SCD} \right)\) tại S nên MP không song song với \(\left( {SCD} \right)\).
Vậy mệnh đề đúng là I; II; IV
