Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AD\) là đáy lớn thỏa mãn \(AD = 2BC\). Các điểm \(M,N\) lần lượt là trung điểm của các cạnh \(SA,\,\,SD\).
a) Chứng minh đường thẳng \(MN\) song song với mặt phẳng \(\left( {SBC} \right)\).
b) Mặt phẳng \(\left( {MCD} \right)\) cắt \(SB\) tại \(E\). Tính tỉ số \(\frac{{SE}}{{EB}}\).
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
a) \[\left\{ \begin{array}{l}a||b\\b \subset \left( P \right)\end{array} \right. \Rightarrow a||\left( P \right)\].
b) Chọn \[SB \subset \left( Q \right)\], tìm \[d = \left( Q \right) \cap \left( {MCD} \right)\], từ đó suy ra \[E = d \cap SB\].
Sử dụng tính chất trọng tâm và định lí Ta-lét.
Cách giải:
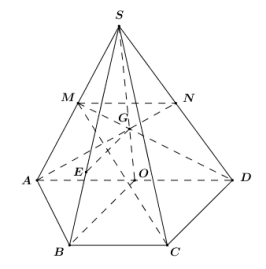
a) Vì \[MN\] là đường trung bình của tam giác \[SAD \Rightarrow MN||AD\] (tính chất đường trung bình).
Mà \[AD||BC\left( {gt} \right) \Rightarrow MN||BC\].
Lại có \[BC \cap \left( {SBC} \right) \Rightarrow MN||\left( {SBC} \right)\].
b) Gọi \[O\] là trung điểm của \[AD\] ta có: \[\left\{ \begin{array}{l}OD = BC = \frac{1}{2}AD\\OD||BC\left( {AD||BC} \right)\end{array} \right. \Rightarrow BCDO\] là hình bình hành \[ \Rightarrow BO||CD\].
Chọn \[SB \subset \left( {SBO} \right)\], tìm giao tuyến của \[\left( {MCD} \right)\] và \[\left( {SBO} \right)\].
+ \[G\] là điểm chung thứ nhất.
\[\left\{ \begin{array}{l}\left( {SBO} \right) \supset BO\\\left( {MCD} \right) \supset CD\\BO||CD\left( {cmt} \right)\end{array} \right.\] Þ Giao tuyến của \[\left( {MCD} \right)\] và \[\left( {SBO} \right)\] là đường thẳng qua \[G\] và song song với \[BO,CD\].
Trong \[\left( {SBO} \right)\] kẻ \[GE||BO\left( {E \in SB} \right) \Rightarrow \left( {MCD} \right) \cap \left( {SBO} \right) = GE\].
Ta có: \[\left\{ \begin{array}{l}E \in SB\\E \in GH \subset \left( {MCD} \right)\end{array} \right. \Rightarrow E = SB \cap \left( {MCD} \right)\].
Xét tam giác \[SAD\] có \[G\] là giao điểm của hai đường trung tuyến
Þ \[G\] là trọng tâm tam giác \[SAD \Rightarrow \frac{{SG}}{{GO}} = 2\].
Do \[GE||OB\] nên áp dụng đinh lí Ta-lét ta có \[\frac{{SE}}{{EB}} = \frac{{SG}}{{GO}} = 2\].