 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Chia cả 2 vế cho \({\cos ^2}x\), đưa phương trình về ẩn \(\tan x\).
- Đưa phương trình về dạng tích.
- Sử dụng phương pháp giải phương trình chứa căn.
- Cô lập \(m\), sử dụng phương pháp dùng BBT để biện luận nghiệm.
Cách giải:
Do \(x \in \left( {0;\frac{\pi }{4}} \right) \Rightarrow \cos x > 0\).
Chia cả 2 vế phương trình cho \({\cos ^2}x\), ta có:
\[{\sin ^2}x - \sin x\cos x - m{\cos ^2}x = 2\sqrt {3\sin x{{\cos }^3}x + m{{\cos }^4}x} \]
\[ \Leftrightarrow {\tan ^2}x - \tan x - m = 2\sqrt {3\tan x + m} \]
\[ \Leftrightarrow {\tan ^2}x + 2\tan x - 3\tan x - m = 2\sqrt {3\tan x + m} \]
\[ \Leftrightarrow \left[ {{{\tan }^2}x - \left( {3\tan x + m} \right)} \right] = 2\sqrt {3\tan x + m} - 2\tan x\]
\[ \Leftrightarrow \left( {\tan x - \sqrt {3\tan x + m} } \right)\left( {\tan x + \sqrt {3\tan x + m} } \right) = 2\left( {\sqrt {3\tan x + m} - \tan x} \right)\]
\[ \Leftrightarrow \left( {\tan x - \sqrt {3\tan x + m} } \right)\left( {\tan x + \sqrt {3\tan x + m} + 2} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}\tan x = \sqrt {3\tan x + m} \\\tan x + \sqrt {3\tan x + m} + 2 = 0\end{array} \right.\]
Do \[x \in \left( {0;\frac{\pi }{4}} \right) \Rightarrow \tan x > 0 \Rightarrow \tan x + \sqrt {3\tan x + m} + 2 > 0{\rm{ }}\forall x \in \left( {0;\frac{\pi }{4}} \right)\].
\[ \Rightarrow \tan x = \sqrt {3\tan x + m} \Leftrightarrow {\tan ^2}x - 3\tan x - m = 0\].
Đặt \[t = \tan x\], vì \[x \in \left( {0;\frac{\pi }{4}} \right) \Rightarrow t \in \left( {0;1} \right)\].
\[ \Rightarrow {t^2} - 3t - m = 0\] với \[t \in \left( {0;1} \right) \Leftrightarrow {t^2} - 3t = m\] với \[t \in \left( {0;1} \right)\].
Xét hàm số \[f\left( t \right) = {t^2} - 3t\] ta có BBT:
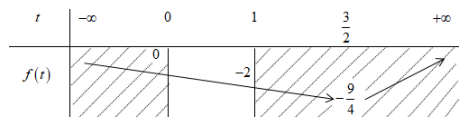
Dựa vào BBT ta thấy phương trình có nghiệm \[t \in \left( {0;1} \right)\] khi và chỉ khi \[ - 2 < m < 0\].
Vậy \[m \in \left( { - 2;0} \right)\].
Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AD\) là đáy lớn thỏa mãn \(AD = 2BC\). Các điểm \(M,N\) lần lượt là trung điểm của các cạnh \(SA,\,\,SD\).
a) Chứng minh đường thẳng \(MN\) song song với mặt phẳng \(\left( {SBC} \right)\).
b) Mặt phẳng \(\left( {MCD} \right)\) cắt \(SB\) tại \(E\). Tính tỉ số \(\frac{{SE}}{{EB}}\).