Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2,1,-2), B(5,1,1) và mặt cầu . Xét đường thẳng d đi qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến d nhỏ nhất. Phương trình của đường thẳng d là
A. .
 Giải bởi Vietjack
Giải bởi Vietjack
Mặt cầu có tâm bán kính .
nên B nằm ngoài (S).
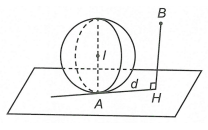
Đường thẳng d đi qua A và tiếp xúc với (S) nên d nằm trong mặt phẳng (P) tiếp xúc với mặt cầu (S) tại A.
Mặt phẳng (P) đi qua A và nhận làm vectơ pháp tuyến có phương trình là .
Gọi H là hình chiếu của B lên (P) thì tọa độ của .
Ta có: .
Vậy khoảng cách từ B đến d nhỏ nhất khi d đi qua H. Ta có .
Suy ra phương trình đường thẳng d là: .
Chọn C.
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm . Khoảng cách giữa AB và CD là
Phương trình đường thẳng d đi qua O và vuông góc với và cách điểm M(3,1,0) một khoảng nhỏ nhất là
Trong không gian Oxyz, khoảng cách giữa đường thẳng và mặt phẳng bằng
Cho phương trình mặt phẳng (P): 2x+y+z-3=0, đường thẳng và điểm . Viết phương trình đường thẳng d đi qua A, nằm trong (P) sao cho khoảng cách d và d' đạt giá trị lớn nhất.
Cho phương trình mặt phẳng (P): 2x+y+z-3=0, đường thẳng và điểm . Viết phương trình đường thẳng d đi qua A, nằm trong (P) sao cho khoảng cách d và d' đạt giá trị lớn nhất.
Trong không gian Oxyz, cho hai điểm M(-2,-2,1), A(1,2,-3) và đường thẳng Tìm vectơ chỉ phương của đường thẳng qua M, vuông góc với đường thẳng d đồng thời cách điểm A một khoảng nhỏ nhất.