Giải bởi Vietjack
Đáp án D
Phương pháp giải:
Dựa vào các yếu tố song song xác định thiết diện.
Giải chi tiết:
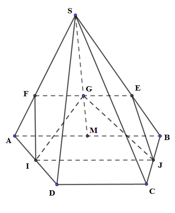
Qua G dựng EF song song AB (\[E \in SB,F \in SA\])
IJ là đường trung bình của hình thang ABCD \[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{IJ{\rm{//}}AB{\rm{//}}CD}\\{IJ = \frac{{AB + CD}}{2}}\end{array}} \right.\]
Ta có: \[\left\{ {\begin{array}{*{20}{l}}{IJ{\rm{//}}AB}\\{AB{\rm{//}}EF}\end{array}} \right. \Rightarrow IJ{\rm{//}}EF \Rightarrow I,J,E,F\] đồng phẳng
\[ \Rightarrow I,J,E,F,G\] đồng phẳng
\[ \Rightarrow \left( {GIJ} \right) \equiv \left( {IJEF} \right)\]
Thiết diện của \[\left( {GIJ} \right)\] với hình chóp là hình thang \[IJEF,{\mkern 1mu} \left( {IJ{\rm{//}}EF} \right)\]
Để thiết diện là hình bình hành thì \[IJ = EF \Leftrightarrow \frac{{AB + CD}}{2} = \frac{2}{3}AB\] (do \[\frac{{EF}}{{AB}} = \frac{{SE}}{{SB}} = \frac{{SG}}{{SM}} = \frac{2}{3}\])
\[ \Leftrightarrow 3AB + 3CD = 4AB \Leftrightarrow AB = 3CD\]
Tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên khoảng \[\left[ { - \frac{\pi }{3};\frac{\pi }{2}} \right]\]
\[y = \cos 2x + \sin {\mkern 1mu} x - \sqrt 3 \left( {\sin 2x + \cos x} \right) + 3\]
