Phương trình \({e^x} - {e^{\sqrt {2x - 1} }} = 1 - {x^2} + 2\sqrt {2x + 1} \) có nghiệm trong khoảng nào sau đây?
D. \(\left( {\frac{3}{2};2} \right)\)
Giải bởi Vietjack
Đáp án B
Phương pháp:
Sử dụng tính đơn điệu của hàm số.
Cách giải:
Điều kiện: \(x \ge - \frac{1}{2}\)
\({e^x} - {e^{\sqrt {2x + 1} }} = 1 - {x^2} + 2\sqrt {2x + 1} \Leftrightarrow 2x + 1 + 2\sqrt {2x + 1} + 1 + {e^{\sqrt {2x + 1} }} = {x^2} + 2x + 1 + {e^x}\)
\( \Leftrightarrow {\left( {\sqrt {2x + 1} + 1} \right)^2} + {e^{\sqrt {2x + 1} }} = {\left( {x + 1} \right)^2} + {e^x}\)
Xét hàm số \(y = {\left( {x + 1} \right)^2} + {e^x} \Rightarrow y' = 2\left( {x + 1} \right) + {e^x} = 2x + 1 + {e^x} + 1 > 0,\,\,\forall x \ge - \frac{1}{2}\)
\( \Rightarrow \) Hàm số đồng biến trên \(\left[ { - \frac{1}{2}; + \infty } \right)\)
Phương trình đã cho tương đương:
\(\sqrt {2x + 1} = x \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\2x + 1 = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} - 2x - 1 = 0\end{array} \right. \Leftrightarrow x = 1 + \sqrt 2 \in \left( {2;\frac{5}{2}} \right)\)
Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \ln x\) trên đoạn \(\left[ {\frac{1}{{{e^2}}};e} \right]\) lần lượt là m và M. Tích M.m bằng
Thể tích của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh \(2\sqrt 2 \) bằng
Cho hình chóp tam giác đều S.ABC với \(SA = \sqrt 6 ,\,\,AB = 3\). Diện tích của mặt cầu có tâm A và tiếp xúc với mặt phẳng (SBC) bằng
Cho lăng trụ tứ giác đều có cạnh bằng a và cạnh bên bằng 2a. Diện tích xung quanh của hình lăng trụ đã cho bằng
Cho biểu thức \(A = {\log _{\sqrt a }}{a^2} + {\log _{\frac{1}{2}}}{4^a},\,\,a > 0,\,\,a \ne 1\). Khẳng định nào sau đây đúng?
Biết rằng phương trình \({5^{2x + \sqrt {1 - 2x} }} - m{.5^{1 - \sqrt {1 - 2x} }} = {4.5^x}\) có nghiệm khi và chỉ khi \(m \in \left[ {a;b} \right]\), với m là tham số. Giá trị của \(b - a\) bằng
Số giao điểm của đồ thị hàm số \(y = {x^3} - 4x + 1\) và đường thẳng \(y = x + 1\) bằng:
Cho hàm số \(y = {\log _2}x\). Xét các phát biểu
(1) Hàm số \(y = {\log _2}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) .
(2) Hàm số \(y = {\log _2}x\) có một điểm cực tiểu.
(3) Đồ thị hàm số \(y = {\log _2}x\) có tiệm cận.
Số phát biểu đúng là
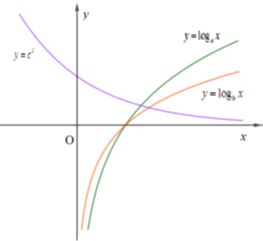
Cho các hàm số \(y = {\log _a}x,\,\,\,y = {\log _b}x\) và \(y = {c^x}\) (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
Tổng tất cả các nghiệm của phương trình \({4^x} - {3.2^{x + 1}} + 8 = 0\)
Phương trình \({3.9^x} - {7.6^x} + {2.4^x} = 0\) có hai nghiệm \({x_1},\,{x_2}\). Tổng \({x_1} + {x_2}\) bằng
Cho khối chóp S.ABC có ba cạnh SA, SB, SC cùng độ dài bằng a và vuông góc với nhau từng đôi một. Thể tích của khối chóp S.ABC bằng
Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng
