Phương trình \({3.9^x} - {7.6^x} + {2.4^x} = 0\) có hai nghiệm \({x_1},\,{x_2}\). Tổng \({x_1} + {x_2}\) bằng
D. –1
Giải bởi Vietjack
Đáp án D
Phương pháp:
Chia cả hai vế cho \({4^x}\), đặt \({\left( {\frac{3}{2}} \right)^x} = t\). Giải phương trình tìm t, từ đó tìm x và tổng \({x_1} + {x_2}\)
Cách giải:
\({3.9^x} - {7.6^x} + {2.4^x} = 0 \Leftrightarrow 3.{\left( {\frac{9}{4}} \right)^x} - 7{\left( {\frac{3}{2}} \right)^x} + 2 = 0\)
Đặt \({\left( {\frac{3}{2}} \right)^x} = t\). Phương trình trở thành \(\begin{array}{l}3{t^2} - 7t + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 2\\t = \frac{1}{3}\end{array} \right. \Rightarrow \left[ \begin{array}{l}{\left( {\frac{3}{2}} \right)^x} = 2\\{\left( {\frac{3}{2}} \right)^x} = \frac{1}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {\log _{\frac{3}{2}}}2\\x = {\log _{\frac{3}{2}}}\frac{1}{3}\end{array} \right.\\\end{array}\)
Tổng hai nghiệm \({x_1} + {x_2} = {\log _{\frac{3}{2}}}2 + {\log _{\frac{3}{2}}}\frac{1}{3} = {\log _{\frac{3}{2}}}\left( {2.\frac{1}{3}} \right) = {\log _{\frac{3}{2}}}\frac{2}{3} = - 1\)
Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \ln x\) trên đoạn \(\left[ {\frac{1}{{{e^2}}};e} \right]\) lần lượt là m và M. Tích M.m bằng
Thể tích của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh \(2\sqrt 2 \) bằng
Cho hình chóp tam giác đều S.ABC với \(SA = \sqrt 6 ,\,\,AB = 3\). Diện tích của mặt cầu có tâm A và tiếp xúc với mặt phẳng (SBC) bằng
Cho lăng trụ tứ giác đều có cạnh bằng a và cạnh bên bằng 2a. Diện tích xung quanh của hình lăng trụ đã cho bằng
Cho biểu thức \(A = {\log _{\sqrt a }}{a^2} + {\log _{\frac{1}{2}}}{4^a},\,\,a > 0,\,\,a \ne 1\). Khẳng định nào sau đây đúng?
Biết rằng phương trình \({5^{2x + \sqrt {1 - 2x} }} - m{.5^{1 - \sqrt {1 - 2x} }} = {4.5^x}\) có nghiệm khi và chỉ khi \(m \in \left[ {a;b} \right]\), với m là tham số. Giá trị của \(b - a\) bằng
Số giao điểm của đồ thị hàm số \(y = {x^3} - 4x + 1\) và đường thẳng \(y = x + 1\) bằng:
Cho hàm số \(y = {\log _2}x\). Xét các phát biểu
(1) Hàm số \(y = {\log _2}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) .
(2) Hàm số \(y = {\log _2}x\) có một điểm cực tiểu.
(3) Đồ thị hàm số \(y = {\log _2}x\) có tiệm cận.
Số phát biểu đúng là
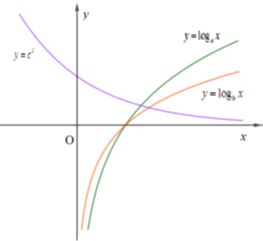
Cho các hàm số \(y = {\log _a}x,\,\,\,y = {\log _b}x\) và \(y = {c^x}\) (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
Tổng tất cả các nghiệm của phương trình \({4^x} - {3.2^{x + 1}} + 8 = 0\)
Cho khối chóp S.ABC có ba cạnh SA, SB, SC cùng độ dài bằng a và vuông góc với nhau từng đôi một. Thể tích của khối chóp S.ABC bằng
Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, \(AB = BC = 2,\,\,AD = 4\); mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng
