Lời giải
Ta có: \(g'\left( x \right) = \left( {3{x^2} - 3} \right)f'\left( {{x^3} - 3x} \right)\).
Suy ra \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} - 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\f'\left( {{x^3} - 3x} \right) = 0\,\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( \~N \right)\\x = - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( \~N \right)\\{x^3} - 3x = - 2\,\,\,\,\left( 1 \right)\\{x^3} - 3x = 1\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\).
Phương trình \(\left( 1 \right) \Leftrightarrow \)\({x^3} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\,\left( {BC} \right)\\x = - 2\,\,\left( {BC} \right)\end{array} \right.\) .
Phương trình \(\left( 2 \right) \Leftrightarrow \)\({x^3} - 3x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x \approx - 1,53 = {x_1}\\x \approx - 0,35 = {x_2}\\x \approx 1,88 = {x_3}\end{array} \right.\).
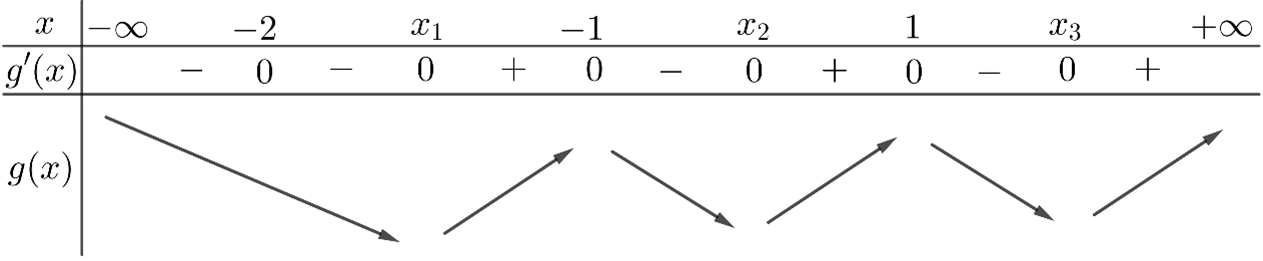
Ta có bảng biến thiên của hàm số \(g\left( x \right)\):
Vậy hàm số \(g\left( x \right)\) có \(3\) điểm cực tiểu.
 Giải bởi Vietjack
Giải bởi Vietjack