Lời giải
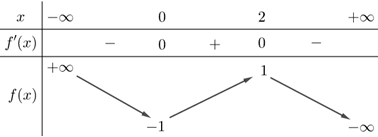
Rõ ràng \(y = \left| {{x^3} - 3x - m} \right| \ge 0\,\,\forall x \in \left[ {0;1} \right]\) suy ra \(\mathop {\min }\limits_{x \in \left[ {0;1} \right]} \,\,y \ge 0\). Dấu “=” xảy ra khi và chỉ khi\({x^3} - 3x - m = 0\) .
Ta tìm \(m \in \mathbb{Z}\) để phương trình \({x^3} - 3x = m\) có nghiệm trong đoạn \(\left[ {0;\,1} \right]\)hay tìm \(m \in \mathbb{Z}\) để đường thẳng \(y = m\) cắt đồ thị hàm số \(y = {x^3} - 3x\) tại điểm có hoành độ thuộc đoạn\(\left[ {0;\,1} \right]\).
Xét \(f\left( x \right) = {x^3} - 3x\) có\({f^'}\left( x \right) = 3\left( {{x^2} - 1} \right) \le 0\,\,\forall x \in \left[ {0;\,1} \right]\) suy ra \[\mathop {Min}\limits_{\left[ {0;1} \right]} f\left( x \right) = f\left( 1 \right) = - 2\],\[\mathop {{\rm{Max}}}\limits_{\left[ {0;1} \right]} f\left( x \right) = f\left( 0 \right) = 0\]. Vậy \[m\] phải thỏa mãn\( - 2 \le m \le 0\).
Vì \(m \in \mathbb{Z}\) nên \(m = 0, - 1, - 2\). Chọn A.
Giải bởi Vietjack
