Lời giải
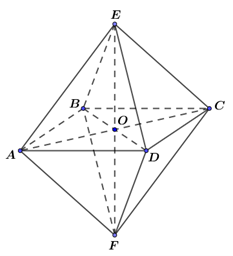
Khối đa diện đều loại \[{\rm{\{ }}3\,;\,\,4\} \] là khối bát diện đều.
Thể tích khối bát diện đều \[{V_{ABCDEF}} = 2.{V_{E.ABCD}}\] với khối chóp \[E.ABCD\] là khối chóp tứ giác đều cạnh bằng \[\sqrt 3 \].
Cách 1. Tính nhanh:
\[{V_{E.ABCD}} = \frac{{{{(\sqrt 3 )}^3}.\sqrt 2 }}{6} = \frac{{\sqrt 6 }}{2}\].
Khi đó \[{V_{ABCDEF}} = 2.{V_{E.ABCD}} = 2.\frac{{\sqrt 6 }}{2} = \sqrt 6 \].
Cách 2. Tự luận
Đáy \[ABCD\] là hình vuông cạnh bằng \[\sqrt 3 \] Þ \[{S_{ABCD}} = {(\sqrt 3 )^2} = 3\].
Đường chéo \[AC = \,\sqrt 3 .\sqrt 2 = \sqrt 6 \] Þ \[OA = \frac{1}{2}AC = \frac{{\sqrt 6 }}{2}\].
Xét \[\Delta EOA\] vuông tại \[O\] có \[EO = \sqrt {E{A^2} - O{A^2}} = \sqrt {{{(\sqrt 3 )}^2} - {{\left( {\frac{{\sqrt 6 }}{2}} \right)}^2}} = \frac{{\sqrt 6 }}{2}\].
\[{V_{E.ABCD}} = \frac{1}{3}.EO.{S_{ABCD}} = \frac{1}{3}.\frac{{\sqrt 6 }}{2}.3 = \frac{{\sqrt 6 }}{2}\].
Khi đó \[{V_{ABCDEF}} = 2.{V_{E.ABCD}} = 2.\frac{{\sqrt 6 }}{2} = \sqrt 6 \].
Giải bởi Vietjack
