 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn D
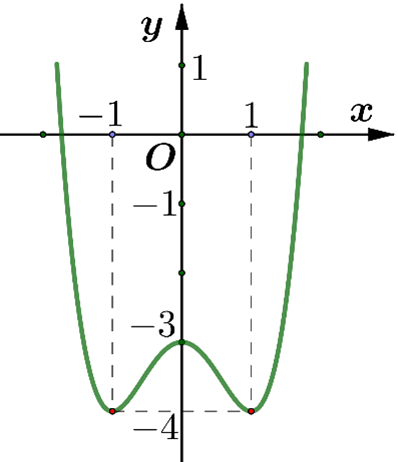
Từ đồ thị hàm số \(y = f\left( x \right)\) ta suy ra đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như sau:
- Giữ nguyên phần đồ thị hàm số \(y = f\left( x \right)\) phía trên trục \(Ox\)
- Phần đồ thị hàm số \(y = f\left( x \right)\) bên dưới trục \(Ox\)được lấy đối xứng qua trục \(Ox\).
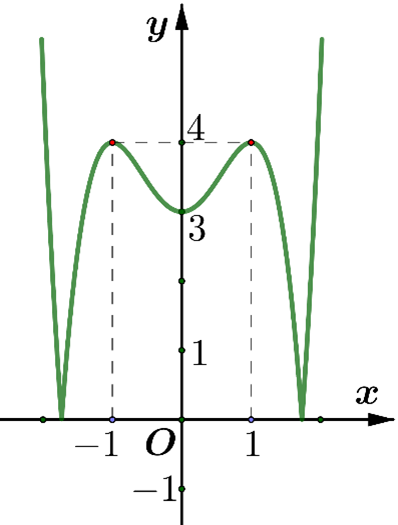
Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m\) là số giao điểm của đồ thị \(y = \left| {f\left( x \right)} \right|\) và đường thẳng\(y = m\).
Từ đồ thị ta thấy phương trình có đúng hai nghiệm phân biệt khi \(\left[ {\begin{array}{*{20}{c}}{m > 4}\\{m = 0}\end{array}} \right.\).