Cho hàm số \(y = f\left( x \right)\)có bảng xét dấu như hình vẽ
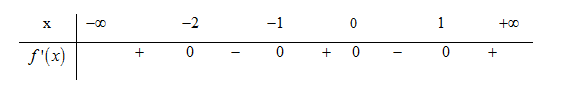
Tìm khoảng đồng biến của hàm số \[y = g(x) = 2f(1 - x) - \frac{1}{5}{x^5} + \frac{5}{4}{x^4} - 3{{\rm{x}}^3}\].
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
Coi \(f'\left( x \right) = \left( {x + 2} \right)\left( {x + 1} \right)x\left( {x - 1} \right)\)có bảng xét dấu như trên.
\[g'(x) = - 2f'(1 - x) - {x^4} + 5{x^3} - 6{{\rm{x}}^2}\]
Ta đi xét dấu \[g'(x) = P + Q\]. Với:
\(P = - 2f'\left( {1 - x} \right) = - 2\left( {3 - x} \right)\left( {2 - x} \right)\left( {1 - x} \right)\left( { - x} \right) = 2x\left( {3 - x} \right)\left( {2 - x} \right)\left( {1 - x} \right)\)
Bảng xét dấu của P
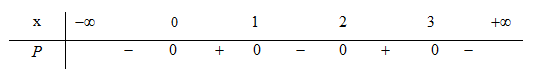
\[Q = - {x^4} + 5{x^3} - 6{{\rm{x}}^2} = - {x^2}\left( {x - 2} \right)\left( {x - 3} \right)\]
Bảng xét dấu của \[Q\]
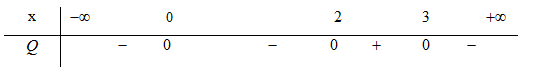
Từ hai BXD của \(P,\,Q\). Ta có \(P > 0,\,Q > 0\)với \(\forall x \in \left( {2;\,3} \right)\)nên \(g'(x) = P + Q > 0\)với \(\forall x \in \left( {2;\,3} \right)\).