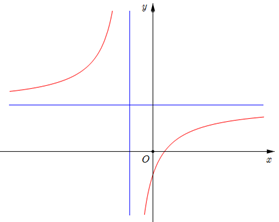
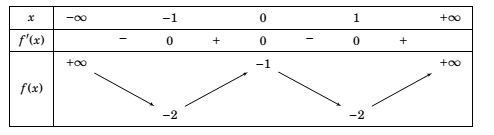
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Hàm số \(g\left( x \right) = 2{f^3}\left( x \right) + 4{f^2}\left( x \right) + 1\) có nhiều nhất bao nhiêu điểm cực tiểu?
Giải bởi Vietjack
Lời giải
Chọn C
Ta có \(g'\left( x \right) = 6{f^2}\left( x \right).f'\left( x \right) + 8f\left( x \right).f'\left( x \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f'\left( x \right) = 0\\f\left( x \right) = - \frac{4}{3}\end{array} \right.\)
Dựa vào bảng biến thiên ta có:
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\), \(f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = {x_2}\end{array} \right.,\) \(f\left( x \right) = - \frac{4}{3} \Leftrightarrow \left[ \begin{array}{l}x = a\\x = b\\x = c\\x = d\end{array} \right.\)
thỏa mãn: \({x_1} < a < - 1 < b < 0 < c < 1 < d < {x_2}\)
Khi đó để có nhiều điểm cực tiếu nhất thì xét dấu của \(g'\left( x \right)\) có dạng:
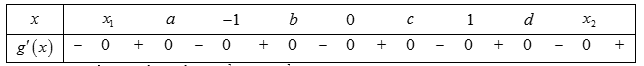
Do đó hàm số có nhiều nhất \(5\) điểm cực tiểu.
