Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
Ta có: \(y' = 4{x^3} - 4x{\mkern 1mu} \).
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 1\end{array} \right.\).
Bảng biến thiên
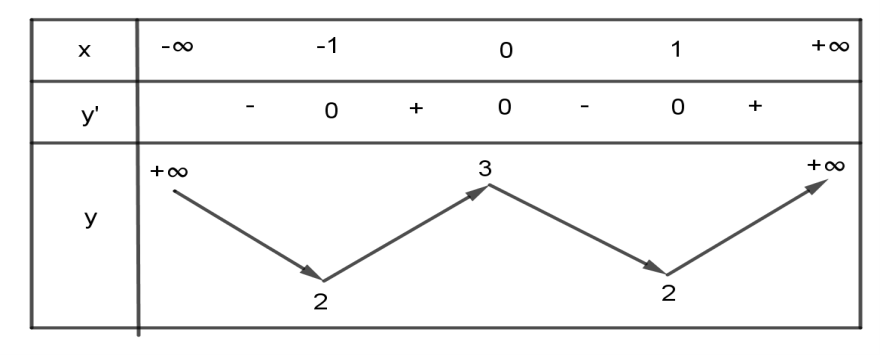
Từ bảng biến thiên ta thấy hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\)và \(\left( {1; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đạo hàm là hàm số \(y = f'\left( x \right)\) với đồ thị như hình vẽ bên.

Biết rằng đồ thị hàm số \(y = f\left( x \right)\) tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?