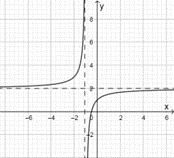
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
Giải bởi Vietjack
Lời giải
Chọn B
Xét đáp án A có \(y' = 0\) \(\forall x \ne - 1\) nên loại.
Xét đáp án B có \(y' = \frac{1}{{{{\left( {x + 1} \right)}^2}}} > 0\) \(\forall x \ne - 1\) \( \Rightarrow \) hàm số đồng biến trên từng khoảng xác định; tiệm cận đứng là \(x = - 1\), tiệm cận ngang là \(y = 2\)nên chọn.
Xét đáp án C: đồ thị hàm số có tiệm cận ngang là đường thẳng \(y = 1\) nên loại.
Xét đáp án D: đồ thị hàm số có tiệm cận đứng là đường thẳng \(x = 1\) nên loại.
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đạo hàm là hàm số \(y = f'\left( x \right)\) với đồ thị như hình vẽ bên.
Biết rằng đồ thị hàm số \(y = f\left( x \right)\) tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?
