Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình vẽ.
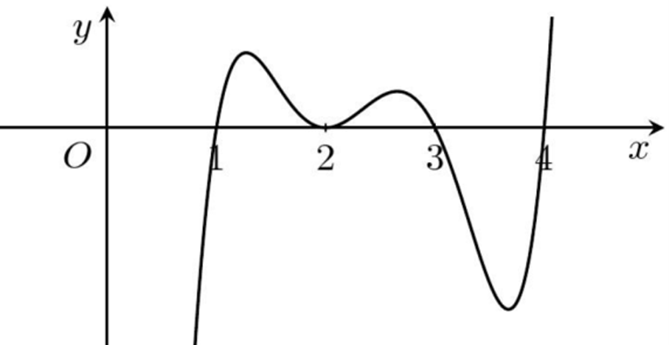
Hàm số \(y = f\left( {{x^2} - 2} \right) - \left( {\frac{{{x^3}}}{3} + {x^2} - 3x + 4} \right)\)nghịch biến trong khoảng nào dưới đây?
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn C
Chọn \(f'\left( x \right) = \left( {x - 1} \right){\left( {x - 2} \right)^2}\left( {x - 3} \right)\left( {x - 4} \right)\)
Đặt \(y = g\left( x \right) = f\left( {{x^2} - 2} \right) - \left( {\frac{{{x^3}}}{3} + {x^2} - 3x + 4} \right)\).
Khi đó \(g'\left( x \right) = 2x.f'\left( {{x^2} - 2} \right) - \left( {{x^2} + 2x - 3} \right)\).
\( = 2x.\left( {{x^2} - 2 - 1} \right){\left( {{x^2} - 2 - 2} \right)^2}\left( {{x^2} - 2 - 3} \right)\left( {{x^2} - 2 - 4} \right) - \left( {{x^2} + 2x - 3} \right)\)\( = 2x.\left( {{x^2} - 3} \right){\left( {{x^2} - 4} \right)^2}\left( {{x^2} - 5} \right)\left( {{x^2} - 6} \right) - \left( {{x^2} + 2x - 3} \right)\)
\(g'\left( { - 2} \right) = 3 > 0\)
\(\,g'\left( 3 \right) = 10788 > 0\)
Cách 2: (TV phản biện)
Ta có \(y' = g'\left( x \right) = 2x.f'\left( {{x^2} - 2} \right) - \left( {{x^2} + 2x - 3} \right)\)
Từ đồ thị ta có \(f'\left( {{x^2} - 2} \right) < 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 2 < 1}\\{3 < {x^2} - 2 < 4}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x \in \left( { - \sqrt 3 ;\sqrt 3 } \right)}\\{x \in \left( { - \sqrt 6 ; - \sqrt 5 } \right) \cup \left( {\sqrt 5 ;\sqrt 6 } \right)}\end{array}} \right.\).
Suy ra \(2xf'\left( {{x^2} - 2} \right) < 0 \Leftrightarrow x \in \left( { - \infty ; - \sqrt 6 } \right) \cup \left( { - \sqrt 5 ; - \sqrt 3 } \right) \cup \left( {0;\sqrt 3 } \right) \cup \left( {\sqrt 5 ;\sqrt 6 } \right)\)
Nên ta lập được bảng xét dấu của \(g'\left( x \right)\)như sau

Từ bảng xét dấu ta thấy hàm số đã cho nghịch biến trên các khoảng \(\left( { - \infty ; - 3} \right)\), \(\left( {1;\sqrt 3 } \right)\)và \(\left( {\sqrt 5 ;\sqrt 6 } \right)\).
Vậy đáp án đúng là đáp án
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đạo hàm là hàm số \(y = f'\left( x \right)\) với đồ thị như hình vẽ bên.

Biết rằng đồ thị hàm số \(y = f\left( x \right)\) tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?