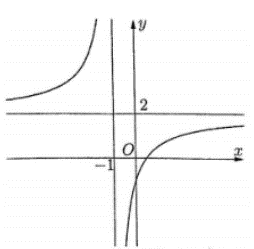
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị trong hình bên. Khẳng định nào dưới đây là sai?
A. Đồ thị hàm số nhận đường thẳng \(x = 2\) là tiệm cận ngang.
B. \(c = d\)
C. Hàm số đồng biến trên khoảng \(\left( {0;5} \right)\)
D. Hàm số không có cực trị.
Giải bởi Vietjack
Đáp án A
Phương pháp:
Dựa vào đồ thị hàm số.
Cách giải:
Đồ thị hàm số nhận đường thẳng \(y = 2\) là tiệm cận ngang và \(x = - 1\) là tiệm cận đứng \( \Rightarrow \) A sai
Đồ thị hàm số nhận đường thẳng \(x = - 1\) là tiệm cận đứng \( \Rightarrow - \frac{d}{c} = - 1 \Leftrightarrow c = d \Rightarrow \) B đúng
Hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\). Có \(\left( {0;5} \right) \subset \left( { - 1; + \infty } \right) \Rightarrow \) Hàm số đồng biến trên khoảng \(\left( {0;5} \right) \Rightarrow \) C đúng
Ta có: \(y' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}} \ne 0\) nên hàm số không có cực trị \( \Rightarrow \) D đúng
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Tính thể tích V của khối cầu ngoại tiếp khối chóp S.ABCD.
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{x\sqrt {4 - {x^2}} }}{{{x^2} - 3x + 2}}\)
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng \({60^0}\). Thể tích V của hình chóp S.ABCD.
Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
Tính khoảng cách d giữa 2 điểm cực trị của đồ thị hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)
Tính khoảng cách d ngắn nhất giữa hai điểm thuộc hai nhánh của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\)
Một hình nón có chiều cao bằng \(\sqrt 5 \), đường kính đáy bằng 6. Tính thể tích V của khối nón đó?
Tìm phương trình các đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{\sqrt {4{x^2} + 1} + 2x}}{x}\)
Cho \(\left( {{C_m}} \right):y = 2{x^3} - \left( {3m + 3} \right){x^2} + 6mx - 4\). Gọi T là tập các giá trị của m thỏa mãn \(\left( {{C_m}} \right)\) có đúng hai điểm chung với Ox, tính tổng S các phần tử của T.
Cho hình chóp S.ABCD, M là trung điểm của SA. Gọi \(\left( \alpha \right)\) là mặt phẳng qua M và song song với mặt phẳng (ABCD). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp S.ABCD thành hai khối gồm khối chứa điểm S có thể tích \({V_1}\) và khối chứa điểm A có thể tích \({V_2}\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)?
Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện tích là 50. Tính bán kính R của hình nón đó?
Tìm m để phương trình \({\log _2}\sqrt {{x^2} - 3x + 2} + {\log _{\frac{1}{2}}}\left( {x - m} \right) = x - m - \sqrt {{x^2} - 3x + 2} \) có nghiệm?
Tìm tất cả các giá trị của tham số m để hàm số \(y = \frac{{x - 2}}{{mx - 1}}\) đồng biến trên \(\left( {1; + \infty } \right)\)
Tìm tất cả các giá trị m để hàm số \(y = mx + 2\sin x - 3\cos \,x\) nghịch biến trên R.
