Có một mô hình kim tự tháp là một chóp tứ giác đều có cạnh bằng 6cm; cạnh đáy bằng 4cm được đặt trên một bàn trưng bày (đáy nằm trên mặt bàn). Một chú kiến tinh nghịch đang ở đỉnh của đáy và có ý định khám phá một vòng qua tất cả các mặt và trở về vị trí ban đầu. Tính quãng đường ngắn nhất của chú kiến (nếu kết quả lẻ thì làm tròn đến 2 chữ số thập phân).
D. \(16\left( {cm} \right)\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Trải tất cả các mặt bên của khối chóp ra cùng một mặt phẳng.
Cách giải:
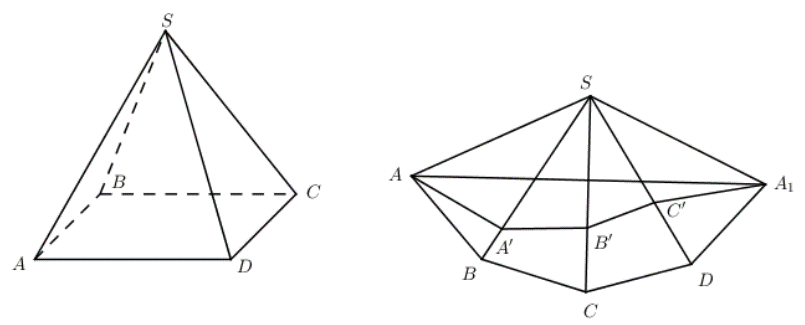
Trải hình chóp S.ABCD trên cùng một mặt phẳng \(\left( {{A_1} \equiv A} \right)\)
Giả sử quãng đường của con kiến đi từ A đến \({A_1}\) là , khi đó quãng đường con kiến đi ngắn nhất là độ dài đoạn \(A{A_1}\)
Xét tam giác SAB có:
\(\cos \angle ASB = \frac{{S{A^2} + S{B^2} - A{B^2}}}{{2SA.SB}} = \frac{{{6^2} + {6^2} - {4^2}}}{{{{2.6}^2}}} = \frac{7}{9}\)
\( \Rightarrow \angle ASB \approx 38,{9^0}\)
\( \Rightarrow \angle AS{A_1} = 4\angle ASB = 155,{8^0}\)
Xét tam giác \(AS{A_1}\) có:
\[{\rm{AA}}_1^2 = S{A^2} + SA_1^2 - 2SA.S{A_1}.{{\mathop{\rm cosASA}\nolimits} _1} \approx 11,73\left( {cm} \right)\]
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Tính thể tích V của khối cầu ngoại tiếp khối chóp S.ABCD.
Tìm tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \frac{{x\sqrt {4 - {x^2}} }}{{{x^2} - 3x + 2}}\)
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng \({60^0}\). Thể tích V của hình chóp S.ABCD.
Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.
Tính khoảng cách d giữa 2 điểm cực trị của đồ thị hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)
Tính khoảng cách d ngắn nhất giữa hai điểm thuộc hai nhánh của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 1}}\)
Tìm m để phương trình \({\log _2}\sqrt {{x^2} - 3x + 2} + {\log _{\frac{1}{2}}}\left( {x - m} \right) = x - m - \sqrt {{x^2} - 3x + 2} \) có nghiệm?
Tìm phương trình các đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{\sqrt {4{x^2} + 1} + 2x}}{x}\)
Một hình nón có chiều cao bằng \(\sqrt 5 \), đường kính đáy bằng 6. Tính thể tích V của khối nón đó?
Thiết diện qua trục của một hình nón là một tam giác vuông cân có diện tích là 50. Tính bán kính R của hình nón đó?
Cho hình chữ nhật ABCD, cạnh \(AB = 8,\,\,AD = 6\). Gọi M, N lần lượt là trung điểm các cạnh BC và AD. Quay hình chữ nhật ABCD quanh đường thẳng MN, ta được một hình tròn xoay. Tính thể tích V của khối tròn xoay đó?
Cho hình chóp S.ABCD, M là trung điểm của SA. Gọi \(\left( \alpha \right)\) là mặt phẳng qua M và song song với mặt phẳng (ABCD). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp S.ABCD thành hai khối gồm khối chứa điểm S có thể tích \({V_1}\) và khối chứa điểm A có thể tích \({V_2}\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)?
Tìm tất cả các giá trị m để hàm số \(y = mx + 2\sin x - 3\cos \,x\) nghịch biến trên R.
Cho \(\left( {{C_m}} \right):y = 2{x^3} - \left( {3m + 3} \right){x^2} + 6mx - 4\). Gọi T là tập các giá trị của m thỏa mãn \(\left( {{C_m}} \right)\) có đúng hai điểm chung với Ox, tính tổng S các phần tử của T.