Cho \(a,b,c,d,e > 0\) Chứng minh : \(a + b + c + d + e \ge \sqrt a \left( {\sqrt b + \sqrt c + \sqrt d + \sqrt e } \right)\)

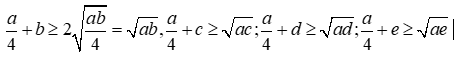
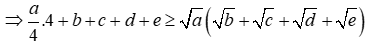
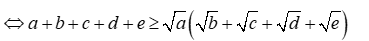
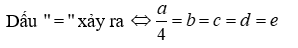
Cho đường tròn tâm \(O\)đường kính \(AB\). Vẽ dây cung \(CD\) vuông góc với \(\)\(AB\) tại \(I(I\)nằm giữa \(A\)và \(O)\).Lấy điểm \(E\)tren cung nhỏ khác \(B\)và \(C),AE\)cắt \(CD\)tại \(F.\)Chứng minh :\(BC(E\)

a.        là tứ giác nội tiếp đường tròn.

b.     \(IA.IB = IC.ID\) và \(AE.AF = A{C^2}\)

c.      Khi \(E\) chạy trên cun nhỏ \(BC\)thì tâm đường tròn ngoại tiếp \(\Delta CEF\) luôn thuộc một đường thẳng cố định.

Một khu vườn hình chữ nhật có chu vi bằng \(72m.\)Nếu tăng chiều rộng lên gấp đôi và chiều dài lên gấp ba thì chu vi của khu vườn mới là \(194m.\)Hãy tìm chiều dài, chiều rộng của khu vườn đã cho lúc ban đầu.

Cho hệ phương trình : \(\left\{ \begin{array}{l}3x - y = 2m - 1\\x + 2y = 3m + 2\end{array} \right.\,\,\,\,\,\,\left( 1 \right)\)

a.        Giải hệ phương trình đã cho khi \(m = 1\)

b.     Tìm \(m\) để hệ \(\left( 1 \right)\) có cặp nghiệm \(\left( {x;y} \right)\) duy nhất thỏa mãn:\({x^2} + {y^2} = 5.\)\(BEFH\)

Trong hệ tọa độ \(Oxy,\) cho đường thẳng \(\left( d \right):\,\,\,y = \left( {a - 2b} \right)x + b.\)Tìm \(a,b\) để \(\left( d \right)\)đi qua \(A\left( {1;2} \right)\)và \(B\left( { - 4; - 3} \right)\)

Cho \(P = \left( {\frac{1}{{x - \sqrt x }} + \frac{{\sqrt x }}{{x - 2\sqrt x + 1}}} \right):\frac{{\sqrt x }}{{x - 2\sqrt {x + 1} }}\) (với \(x > 0,x \ne 1\)

a.        Rút gọn biểu thức \(P.\)

b.     Tính giá trị của \(\left( P \right)\) biết \(x = \frac{2}{{2 - \sqrt {3.} }}\)

c.      Tìm các giá trị của \(x\) để \(P > \frac{1}{2}\)