1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình : Quãng đường Thanh Hóa – Hà Nội dài \(150km.\)Một ô tô từ Hà Nội vào Thanh Hóa, nghỉ lại Thanh Hóa 3 giờ 15 phút, rồi trở về Hà Nội, hết tất cả 10 giờ. Tính vận tốc của ô tô lúc về, biết rằng vận tốc lúc đi lớn hơn vận tốc lúc về là \(10km/h\)
2) Một hình trụ có bán kính đường tròn đáy là \(6cm,\)chiều cao \(9cm.\)Hãy tính diện tích xung quanh của hình trụ.
 Giải bởi Vietjack
Giải bởi Vietjack
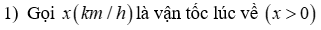
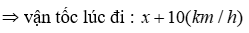

Với \(a,b,c\)là các số dương thỏa mãn \(ab + bc = 2ac.\)Tính giá trị nhỏ nhất của biểu thức : \(P = \frac{{a + b}}{{2a - b}} + \frac{{c + b}}{{2c - b}}\)
Cho nửa đường tròn \(\left( O \right)\), đường kính \(AB.\)Lấy \(M\)bất kỳ thuộc nửa đường tròn (không trùng với \(A,B)\)và C là điểm chính giữa cung \(AM.\)Gọi \(D\)là giao điểm của \(AC\)và \(BM;H\)là giao điểm của \(AM\)và \(BC\)
1) Chứng minh tứ giác \(CHMD\)nội tiếp
2) Chứng minh \(DA.DC = DB.DM\)
3) Gọi \(Q\)là giao điểm của \(DH\)và \(AB.\)Chứng minh khi điểm \(M\)di chuyển trên nửa đường tròn thì đường tròn ngoại tiếp \(\Delta CMQ\)luôn đi qua một điểm cố định.
Cho biểu thức \(A = \frac{{\sqrt x + 1}}{{\sqrt x }}\)và \(B = \left( {\frac{{\sqrt x }}{{\sqrt x - 1}} - \frac{1}{{x - \sqrt x }}} \right):\left( {\frac{1}{{\sqrt x + 1}} + \frac{2}{{x - 1}}} \right)\)\(\left( \begin{array}{l}x > 0\\x \ne 1\end{array} \right)\)
1) Tính giá trị của A khi \(x = 16\)
2) Chứng minh rằng \(B = \frac{{x - 1}}{{\sqrt x }}\)
3) Tìm \(x\)nguyên để \(P = A:B\)đạt giá trị lớn nhất
1) Giải hệ phương trình sau :\(\left\{ \begin{array}{l}\frac{7}{{x - 1}} - \frac{4}{y} = \frac{5}{{13}}\\\frac{5}{{x - 1}} + \frac{3}{y} = \frac{{13}}{6}\end{array} \right.\)
2) Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 3m + 3 = 0 & & \left( 1 \right)\)
a) Giải phương trình với \(m = 3\)
b) Tìm \(m\)để phương trình \(\left( 1 \right)\)có hai nghiệm phân biệt \({x_1},{x_2}\)thỏa mãn \(x_1^2 + x_2^2 = 3\left( {{x_1} + {x_2}} \right) - 2\)