Cho các biểu thức :
\(A = \frac{{\sqrt x + 2}}{{\sqrt x }}\)và \(B = \frac{x}{{x - 4}} + \frac{1}{{\sqrt x - 2}} + \frac{1}{{\sqrt x + 2}}\left( \begin{array}{l}x > 0\\x \ne 4\end{array} \right)\)
1) Tính giá trị của biểu thức \(A\,\,\,khi\,\,\,x = 3 - 2\sqrt 2 \)
2) Rút gọn \(B\)
3) Tìm \(x\)thỏa mãn \(x.P \le 10\sqrt x - 29 - \sqrt {x - 25} \)với \(P = \frac{A}{B}\)
Giải bởi Vietjack
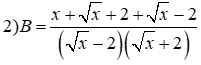
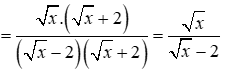
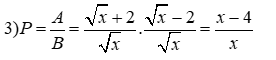
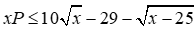
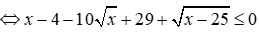
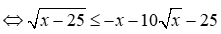
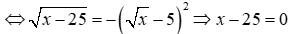
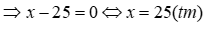
Cho 3 điểm \(A,B,C\)cố định và thẳng hàng theo thứ tự đó. Một đường tròn \(\left( O \right)\)thay đổi nhưng luôn đi qua B và C sao cho \(B,O,C\)không thẳng hàng. Từ A vẽ hai tiếp tuyến \(AM,AN\)với đường tròn \(\left( O \right)\left( {M,N \in \left( O \right)} \right.\)sao cho N thuộc cung nhỏ \(\left. {BC} \right)\)
1) Chứng minh tứ giác \(AMON\)là tứ giác nội tiếp
2) Chứng minh \(AB.AC = A{N^2}\)
3) Gọi \(D\)là trung điểm của \(BC,\)đường thẳng \(ND\)cắt \(\left( O \right)\)tại điểm thứ hai \(E.\)Chứng minh \(ME//AC\)
4) Gọi \(G,H\)theo thứ tự là giao điểm của \(AC,AO.\)Chứng minh \(MN\)luôn đi qua một điểm cố định và tâm đường tròn ngoại tiếp \(\Delta OHG\)luôn nằm trên một đường thẳng cố định.
Giải bài toán bằng cách lập hệ phương trình :
Một ca nô đi xuôi theo một khúc sông trong 3 giờ rồi đi ngược khúc sông đó trong 1 giờ thì được \(190km.\)Một lần khác, cũng trên khúc sông này, ca nô đi xuôi dòng trong 2 giờ và ngược dòng trong 3 giờ thì được \(227km.\)Hãy tính vận tốc riêng của ca nô và vận tốc của dòng nước, biết vận tốc riêng của cano và vận tốc của dòng nước ở hai lần là như nhau.
Cho \(x,y > 0\)và \(x + y = 1.\)Tìn GTNN của biểu thức \(A = \frac{1}{{{x^2} + {y^2}}} + \frac{1}{{xy}}\)
Cho phương trình 2x - y = 5. Phương trình nào sau đây kết hợp với phương trình đã cho được một hệ phương trình có vô số nghiệm ?
1) Giải hệ phương trình sau : \(\left\{ \begin{array}{l}\sqrt {x + 1} + \frac{1}{{x - y}} = 1\\\sqrt {x + 1} - \frac{2}{{x - y}} = 4\end{array} \right.\)
2) Cho Parabol \(\left( P \right):y = {x^2}\)và đường thẳng \(\left( d \right):y = \left( {2m + 1} \right)x - {m^2} - m + 2\left( m \right.\)là tham số)
a) Tìm tọa độ giao điểm của \(\left( P \right),\left( d \right)\)với \(m = 3\)
b) Chứng minh rằng đường thẳng \(\left( d \right)\)luôn cắt Parabol \(\left( P \right)\)tại hai điểm phân biệt với mọi giá trị của \(m.\)Gọi \({x_1},{x_2}\)là hoành độ của hai giao điểm đó, tìm \(m\)để \( - 3 < {x_1} < {x_2} < 3\)
