Cho hình chóp S.ABCD. Gọi M, N, P là các điểm trên SA, SB, SC. Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD).
Giải bởi Vietjack
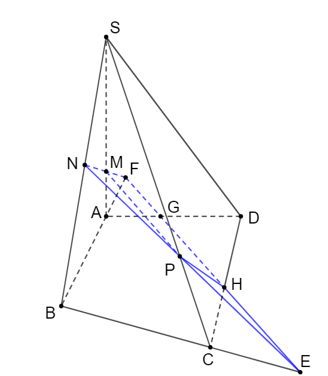
Lấy F và E lần lượt là giao điểm của NM với AB và NP với BC.
Lấy G và H lần lượt là giao điểm của FE với AD và CD.
Vậy giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) là giao tuyến của mặt phẳng (NME) với mặt phẳng (ABCD), tức là GH.
Cho đường tròn tâm O và điểm A nằm bên ngoài đường tròn, từ A vẽ tiếp tuyến AB với đường tròn (B là tiếp điểm). Kẻ đường kính BC của đường tròn (O). AC cắt đường tròn (O) tại D (D khác C).
a) Chứng minh: BD ^ AC và AB2 = AD.AC.
Từ điểm P nằm ngoài đường tròn (O; R) vẽ 2 tiếp tuyến PA, PB tới (O) với A, B là các tiếp điểm. Vẽ AH vuông góc với đường kính BC. Chứng minh PC cắt AH tại trung điểm I của AH.
Từ điểm P nằm ngoài đường tròn tâm O bán kính R, kẻ hai tiếp tuyến PA, PB tới đường tròn (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A tới đường kính BC, đoạn thẳng PC cắt AH tại E.
Cho đường tròn (O) tâm O đường kính AB lấy điểm C thuộc đường tròn (O), với C không trùng A và B. Gọi I là trung điểm của AC. Vẽ tiếp tuyến của đường tròn (O) tại điểm C cắt tia OI tại điểm D.
a) Chứng minh OI // BC.
Tìm số tự nhiên có 3 chữ số biết rằng nếu viết thêm 1 chữ số 0 vào giữa chữ số hàng trăm và hàng chục của số đó ta được số mới gấp 6 lần số phải tìm.
Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho . Biết chu vi tam giác MAB là 24 cm, tính độ dài bán kính đường tròn.
Cho hình thoi ABCD, có . Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh 5 điểm E, F, G, H, B, D cùng thuộc một đường tròn
Từ các chữ số 1, 2 , 3, 4, 5, 7, 8, 9 có thể lập được bao nhiêu số tự nhiên, mỗi số gồm 6 chữ số khác nhau và tổng các chữ số hàng chục, hàng trăm, hàng nghìn bằng 8.
Cho đường thẳng (d): y = (m + 1)x + 2m − 3. Chứng minh rằng với mọi m đường thẳng (d) luôn luôn đi qua một điểm cố định. Xác định điểm cố định đó.
Xác định parabol y = ax2 + bx + c, (a ≠ 0), biết rằng đỉnh của parabol đó có tung độ bằng −25, đồng thời parabol đó cắt trục hoành tại hai điểm A(−4; 0) và B(6; 0).
