Cho ∆ABC vuông tại A, kẻ đường cao AH. Gọi I, J là trung điểm của AH và HC. Chứng minh rằng: BI ⊥ AJ.
Giải bởi Vietjack
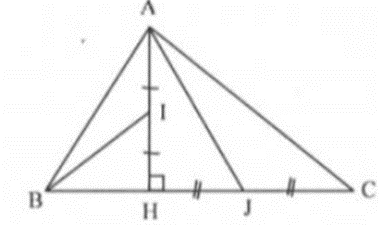
Ta có: \(\overrightarrow {{\rm{AJ}}} = \frac{1}{2}\left( {\overrightarrow {AH} + \overrightarrow {AC} } \right);\overrightarrow {BI} = \frac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BH} } \right)\)
\(\overrightarrow {AJ} .\overrightarrow {BI} = \frac{1}{4}\left( {\overrightarrow {AH} + \overrightarrow {AC} } \right)\left( {\overrightarrow {BA} + \overrightarrow {BH} } \right) = \frac{1}{4}\left( {\overrightarrow {AH} .\overrightarrow {BA} + \overrightarrow {AH} .\overrightarrow {BH} + \overrightarrow {AC} .\overrightarrow {BA} + \overrightarrow {AC} .\overrightarrow {BH} } \right)\)
\( = \frac{1}{4}\left( {\overrightarrow {AH} .\overrightarrow {HA} + 0 + 0 + \overrightarrow {HC} .\overrightarrow {BH} } \right) = \frac{1}{4}\left( { - A{H^2} + BH.HC} \right)\)
Vì ∆ABC vuông tại A nên: \(A{H^2} = HB.HC\)
Do đó: \(\overrightarrow {AJ} .\overrightarrow {BI} = 0 \Leftrightarrow AJ \bot BI\).
Viết chương trình nhập số nguyên dương n. Kiểm tra n có phải là số nguyên tố hay không ?
– Input: 3
– Output: 3 là số nguyên tố
Cho (O; R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A vẽ 2 tiếp tuyến AB, AC của đường tròn (O) (B, C là tiếp điểm). Vẽ dây BE của đường tròn (O) song song với AC; AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của đoạn DE.
a. Chứng minh 5 điểm A, B, C, O, M cùng thuộc 1 đường tròn
b. Chứng minh \(S{C^2}\)= SB.SD
c. 2 đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H. Chứng minh 3 điểm H, O, C thẳng hàng.
Một vòi nước chảy vào cái bể không có nước trong 2h. Giờ đầu vòi chảy được \(\frac{1}{4}\)bể, giờ sau chảy được\(\frac{1}{6}\)bể. Người ta đã dùng lượng nước \(\frac{1}{3}\)bể. Hỏi lượng nước chiếm mấy phần bể ?
Một của hàng bán vật liệu xây dựng có 127,5 tạ xi măng. Buổi sáng cửa hàng bán được \(\frac{1}{5}\) lượng xi măng đó, buổi chiều bán được \(\frac{1}{5}\) lượng xi măng còn lại. Hỏi cả sáng và chiều của hàng đó bán được bao nhiêu tạ xi măng ?
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường trong (O) lấy 1 điểm C sao cho AC < BC. Tiếp tuyến tại C của đường tròn (O) cắt Ax, By lần lượt tại E và F.
a. Chứng minh EF = AE + BF
c. BC cắt Ax tại D. Chứng minh \(A{D^2} = DC.DB\)
Lớp 5A có số học sinh giỏi bằng \(\frac{1}{3}\)số học sinh cả lớp. Số học sinh khá bằng \(\frac{3}{7}\) số học sinh cả lớp. Số học sinh trung bình bằng \(\frac{1}{6}\) số học sinh cả lớp và còn lại 3 em học sinh kém. Hỏi lớp 5A có bao nhiêu học sinh giỏi?
Tìm nghiệm âm lớn nhất của phương trình \(\sin x + \cos x = 1 - \frac{1}{2}\sin 2x\).
Một cửa hàng ngày thứ nhất bán được 35,5 mét vải, ngày thứ hai bán gấp đôi ngày thứ nhất và kém ngày thứ ba 3 mét. Hỏi cả ba ngày cửa hàng đó bán được bao nhiêu mét vải ?
Giả sử x và y là các biến số. Hãy cho biết kết quả của việc thực hiện thuật toán sau:
Bước 1: x ← x + y
Bước 2: y ← x – y
Bước 3: x ← x – y
Hoàn thiện chương trình dưới đây, chương trình nhập từ bàn phím 3 số thực a, b, c đưa ra thông điệp “Cả 3 số đều dương” nếu cả 3 số đều dương.
|
Chương trình |
Kết quả chạy với a bằng 8 |
|
a = …. (input(“a=”)) b = …. (input(“b=”)) c = …. (input(“c=”)) if ….: print(“Cả ba số đều dương”) |
A = 8 B = 4 C = 5 Cả ba số đều dương |
Cho α là góc tù và sinα – cosα = \(\frac{4}{5}\). Giá trị của M = sinα – 2cosα là ?
Cho ∆ABC có \(\widehat B = 60^\circ ,\widehat C = 40^\circ ,BC = 6cm.\)Tính:
a. Đường cao AH và cạnh AC.
b. Tính diện tích ∆ABC.
