Xét dấu của các tam thức bậc hai sau:
a) x2 + 8x + 16;
b) −2x2 + 7x – 3.
Giải bởi Vietjack
a) f(x) = x2 + 8x + 16
Ta có \(\Delta '\)= 42 – 1.16 = 0; hệ số a = 1 > 0 nên f(x) có nghiệm kép x = −4 và f(x) > 0 với mọi m ≠ −4.
b) f(x) = −2x2 + 7x – 3
Ta có \(\Delta \)= 72 – 4.(−2).(−3) = 25 > 0, hệ số a = −2 < 0 và có hai nghiệm phân biệt \({x_1} = \frac{1}{2}\); x2 = 3.
Do đó ta có bảng xét dấu f(x):
|
x |
\( - \infty \) \(\frac{1}{2}\) 3 \( + \infty \) |
|
f(x) |
− 0 + 0 − |
Suy ra f(x) > 0 \(\forall x \in \left( {\frac{1}{2};3} \right)\) và f(x) < 0 \(\forall x \in \left( { - \infty ;\frac{1}{2}} \right) \cup (3; + \infty )\).
Cho đường tròn (O; 4 cm), đường kính AB. Lấy điểm H thuộc đoạn AO sao cho OH = 1 cm. Kẻ dây cung DC vuông góc với AB tại H.
a) Chứng minh ∆ABC vuông và tính độ dài AC.
b) Tiếp tuyến tại A của (O) cắt BC tại E. Chứng minh ∆CBD cân và \(\frac{{EC}}{{DH}} = \frac{{EA}}{{DB}}\).
c) Gọi I là trung điểm của EA; đoạn IB cắt (O) tại Q. Chứng minh CI là tiếp tuyến của (O) cà từ đó suy ra \(\widehat {ICQ} = \widehat {CBI}\).
d) Tiếp tuyến tại B của (O) cắt IC tại F. Chứng minh ba đường thẳng IB, HC, AF đồng quy.
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HE vuông góc với AB và kẻ HF vuông góc với AC.
a) CM: AE.AB = AF.AC;
b) Cho biết AB = 4 cm, AH = 3 cm. Tính AE và BE;
c) Cho biết \[\widehat {HAC} = 30^\circ \]. Tính FC.
Cho đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm của OA, qua C kẻ đường thẳng vuông góc với OA cắt đường tròn (O) tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K (K khác B và M). Gọi H là giao điểm của AK và MN.
a) Chứng minh tứ giác BCHK nội tiếp đường tròn.
b) Chứng minh AK.AH = R2.
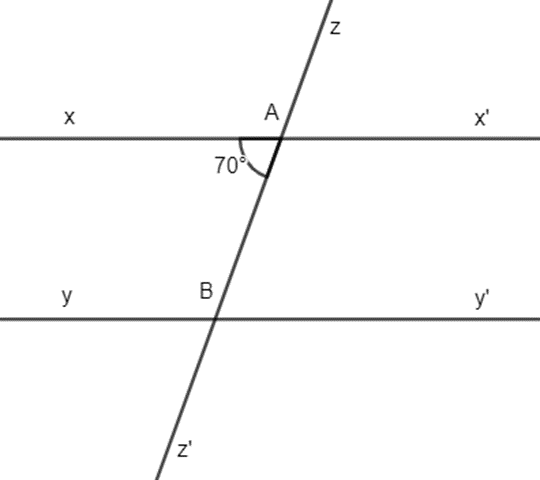
Cho hình vẽ biết xx’ // yy’ và \(\widehat {xAB} = 70^\circ \). Tính số đô góc \(\widehat {yBz'}\) và \(\widehat {ABy}\).
Cho 6 điểm A, B, C, D, E, F. Tổng \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} \) bằng:
Viết tập hợp A là các số \(x\,\, \vdots \,\,5\), thỏa mãn 124 < x < 145 bằng cách liệt kê các phần tử.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Chứng minh: AB2 = AH.BC.
Cho hình vẽ:
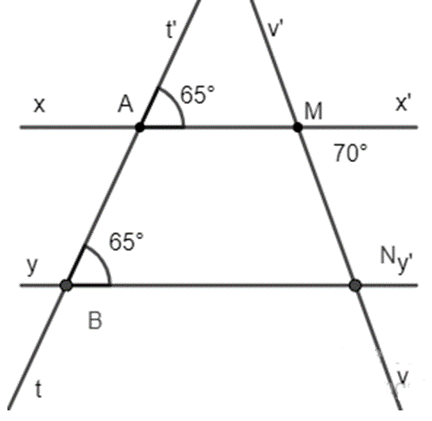
a) Giải thích tại sao xx’ // yy’.
b) Tính số đo \(\widehat {MNB}\).
Cho đường tròn (O) bán kính OA = 4 cm. Dây BC vuông góc với OA tại trung điểm của OA. Tính độ dài BC.
1) Xác định hàm số y = ax + b, biết rằng đồ thị hàm số đi qua hai điểm
A(2; −4) và B(−1; 5).
2) Trên hệ trục tọa độ Oxy, vẽ đồ thị hàm số y = −2x + 1.
Rút gọn biểu thức:
S = cos(90° − x).sin(180° − x) – sin(90° − x).cos(180° − x).
Hai bạn An và Khang đi mua 18 gói bánh và 12 gói kẹo để đến lớp ăn liên hoan. An đưa cho cô bán hàng 4 tờ 50 000 đồng và đc trả lại 72 000 đồng. Khang nói "cô tính sai rồi". Em hãy cho biết Khang nói đúng hay sai? Giải thích tại sao?
