Để tính diện tích tam giác cân, người Ai Cập cổ lấy nửa đáy nhân với cạnh bên. Nếu 1 tam giác cân có cạnh đáy bằng 4m, cạnh bên 10m thì sai số trong cách tính trên so với cách tính đúng là bao nhiêu phần trăm?
Giải bởi Vietjack
Gọi tam giác cân trên là ABC cân tại A
Suy ra BC = 4, AB = AC = 10
Theo cách tính của người Ai Cập, ta có SABC = \(\frac{1}{2}\) . 4 . 10 = 20 (m2)
Kẻ AH vuông góc với BC tại H
Mà tam giác ABC cân tại A
Suy ra H là trung điểm BC
Do đó HB = HC = 2
Áp dụng Pytago cho tam giác vuông AHB ta có
AH2 + HB2 = AB2
Hay AH2 + 22 = 102
Suy ra AH = \(4\sqrt 6 \) (m)
Theo cách tính bây giờ: SABC = \(\frac{1}{2}\) . \(4\sqrt 6 \) . 4 = \(8\sqrt 6 \) (m2)
Suy ra sai số = \(\frac{{20}}{{8\sqrt 6 }}.100\% = 102\% \)
Vậy diện tính tính bởi người Ai Cập sẽ lớn hơn diện tích thật 2%.
a) Chứng minh DE = BF.
b) Tia DE cắt BF tại H. Chứng minh \(\widehat {DHF}\) = 90°
c) Gọi I là trung điểm của EF, K là giao điểm của FE và BD. Chứng minh tứ giác AOIK là hình bình hành.
d) Chứng minh A, H, K thẳng hàng.
Cho tam giác ABC có AB = 2, BC = 4, CA = 3.
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \), rồi suy ra cosA
b) Gọi G là trọng tâm của △ABC. Tính \(\overrightarrow {AG} .\overrightarrow {BC} \)
c) Tính giá trị biểu thức S = \(\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} \)
d) Gọi AD là phân giác trong của góc BAC (D ∈ BC). Tính \(\overrightarrow {A{\rm{D}}} \) theo \(\overrightarrow {AB} ;\overrightarrow {AC} \)suy ra AD.
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.
a) Chứng minh: \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \)
b) Tìm các điểm D, C sao cho \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ;\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
Cho (O;R) đường kính AD, dây AB , qua B kẻ dây BC vuông góc AD tại H . Tính bán kính R của đường tròn biết AB = 10 cm, BC = 12 cm.
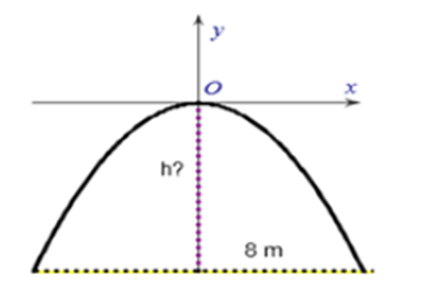
Một chiếc cổng hình parabol dạng y = \( - \frac{1}{2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh)
Một số nếu giảm xuống 3 lần rồi bớt đi 14,6 thì được kết quả là 30,4. Tìm số đó.
Cho 5 điểm A, B, C, D, E. Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {E{\rm{A}}} = \overrightarrow {CB} + \overrightarrow {E{\rm{D}}} \).
b) \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} = \overrightarrow {A{\rm{E}}} - \overrightarrow {DB} + \overrightarrow {CB} \).
Cho tứ giác ABCD. Tìm điểm O sao cho \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {O{\rm{D}}} = \overrightarrow 0 \)
Cho nửa đường tròn (O) đường kính AD. Trên nửa đường tròn lấy hai điểm B và C, biết AB = BC = \(2\sqrt 5 \) cm, CD = 6 cm. Tìm bán kính đường tròn.
Xác định đường thẳng đi qua A(4 ; 3), cắt trục tung tại điểm có tung độ là 1 số nguyên dương, cắt trục hoành tại 1 điểm có hoành độ là 1 số nguyên tố.
Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)
Cho 4 điểm A, B, C, D bất kì. Chứng minh \(\overrightarrow {AB} + \overrightarrow {C{\rm{D}}} = \overrightarrow {A{\rm{D}}} + \overrightarrow {CB} \).
Tìm x, y, z biết \(\frac{{x - 1}}{2} = \frac{{y + 3}}{4} = \frac{{z - 5}}{6}\) và 5z – 3x – 4y = 50.
Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường hợp này là tứ giác có hình ảnh cánh diều)
a) Chứng minh AC là đường trung trực của BD
b) Tính góc B và góc D (biết \(\widehat A = 100^\circ ,\widehat C = 60^\circ \)).
