Tìm tập xác định của hàm số sau:
a) y = 3x2 – 2x + 1
b) y = \(\frac{{3\left| x \right| + 2}}{{x - 2}}\)
c) y = \(\sqrt {x - 2} + \sqrt {3 - x} \)
d) y = \(\frac{{\frac{{2{\rm{x}} - 1}}{{\sqrt {4 - 3{\rm{x}}} }}}}{x}\)
e) y = \(\frac{{\sqrt {x + 3} }}{{2 - x}}\)
f) y = \(\frac{{2{\rm{x}} + 1}}{{{x^2} - 3{\rm{x}} + 2}}\)
g) y = \(\frac{{x - 1}}{{{x^2} - 1}} - 3x\)
Giải bởi Vietjack
a) y = 3x2 – 2x + 1
Hàm số xác định với mọi x ∈ R
Vậy tập xác định D = R.
b) y = \(\frac{{3\left| x \right| + 2}}{{x - 2}}\)
Hàm số xác định khi x – 2 ≠ 0
Hay x ≠ 2
Vậy tập xác định D = R \ {2}.
c) y = \(\sqrt {x - 2} + \sqrt {3 - x} \)
Hàm số xác định khi \(\left\{ \begin{array}{l}x - 2 \ge 0\\3 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \le 3\end{array} \right. \Leftrightarrow 2 \le {\rm{x}} \le 3\)
Vậy tập xác định D = [2; 3].
d) y = \(\frac{{\frac{{2{\rm{x}} - 1}}{{\sqrt {4 - 3{\rm{x}}} }}}}{x}\)
Hàm số xác định khi \(\left\{ \begin{array}{l}4 - 3x > 0\\x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < \frac{4}{3}\\x \ne 0\end{array} \right.\)
Vậy tập xác định D = (– ∞; \(\frac{4}{3}\)) \ {0}.
e) y = \(\frac{{\sqrt {x + 3} }}{{2 - x}}\)
Hàm số xác định khi \(\left\{ \begin{array}{l}x + 3 > 0\\2 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 3\\x \ne 2\end{array} \right.\)
Vậy tập xác định D = (– 3; + ∞) \ {2}.
f) y = \(\frac{{2{\rm{x}} + 1}}{{{x^2} - 3{\rm{x}} + 2}}\)
Hàm số xác định khi x2 – 3x + 2 ≠ 0
⇔ (x – 1)(x – 2) ≠ 0
⇔ \(\left\{ \begin{array}{l}x \ne 1\\x \ne 2\end{array} \right.\)
Vậy tập xác định D = R \ {1; 2}.
g) y = \(\frac{{x - 1}}{{{x^2} - 1}} - 3x\)
Hàm số xác định khi x2 – 1 ≠ 0
⇔ \(\left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right.\)
Vậy tập xác định D = R \ {1; –1}.
a) Chứng minh DE = BF.
b) Tia DE cắt BF tại H. Chứng minh \(\widehat {DHF}\) = 90°
c) Gọi I là trung điểm của EF, K là giao điểm của FE và BD. Chứng minh tứ giác AOIK là hình bình hành.
d) Chứng minh A, H, K thẳng hàng.
Cho tam giác ABC có AB = 2, BC = 4, CA = 3.
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \), rồi suy ra cosA
b) Gọi G là trọng tâm của △ABC. Tính \(\overrightarrow {AG} .\overrightarrow {BC} \)
c) Tính giá trị biểu thức S = \(\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} \)
d) Gọi AD là phân giác trong của góc BAC (D ∈ BC). Tính \(\overrightarrow {A{\rm{D}}} \) theo \(\overrightarrow {AB} ;\overrightarrow {AC} \)suy ra AD.
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.
a) Chứng minh: \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \)
b) Tìm các điểm D, C sao cho \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ;\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
Cho (O;R) đường kính AD, dây AB , qua B kẻ dây BC vuông góc AD tại H . Tính bán kính R của đường tròn biết AB = 10 cm, BC = 12 cm.
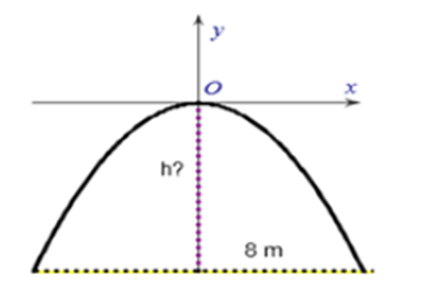
Một chiếc cổng hình parabol dạng y = \( - \frac{1}{2}{x^2}\) có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (Xem hình minh họa bên cạnh)
Một số nếu giảm xuống 3 lần rồi bớt đi 14,6 thì được kết quả là 30,4. Tìm số đó.
Cho 5 điểm A, B, C, D, E. Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {E{\rm{A}}} = \overrightarrow {CB} + \overrightarrow {E{\rm{D}}} \).
b) \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} = \overrightarrow {A{\rm{E}}} - \overrightarrow {DB} + \overrightarrow {CB} \).
Cho tứ giác ABCD. Tìm điểm O sao cho \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {O{\rm{D}}} = \overrightarrow 0 \)
Cho nửa đường tròn (O) đường kính AD. Trên nửa đường tròn lấy hai điểm B và C, biết AB = BC = \(2\sqrt 5 \) cm, CD = 6 cm. Tìm bán kính đường tròn.
Xác định đường thẳng đi qua A(4 ; 3), cắt trục tung tại điểm có tung độ là 1 số nguyên dương, cắt trục hoành tại 1 điểm có hoành độ là 1 số nguyên tố.
Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AD} + \overrightarrow {EB} + \overrightarrow {CF} \)
Cho 4 điểm A, B, C, D bất kì. Chứng minh \(\overrightarrow {AB} + \overrightarrow {C{\rm{D}}} = \overrightarrow {A{\rm{D}}} + \overrightarrow {CB} \).
Tìm x, y, z biết \(\frac{{x - 1}}{2} = \frac{{y + 3}}{4} = \frac{{z - 5}}{6}\) và 5z – 3x – 4y = 50.
Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường hợp này là tứ giác có hình ảnh cánh diều)
a) Chứng minh AC là đường trung trực của BD
b) Tính góc B và góc D (biết \(\widehat A = 100^\circ ,\widehat C = 60^\circ \)).
