Cho tam giác ABC. Dựng phía ngoài tam giác các tam giác đều ABC', BCA', CAB'. Gọi M, N, P lần lượt là trung điểm của CA’, AB’, AC’. Chứng minh rằng:
a) MN = PC.
b) Gọi O là giao điểm của MN và PC. Chứng minh \(\widehat {MOC} = 60^\circ \).
 Giải bởi Vietjack
Giải bởi Vietjack
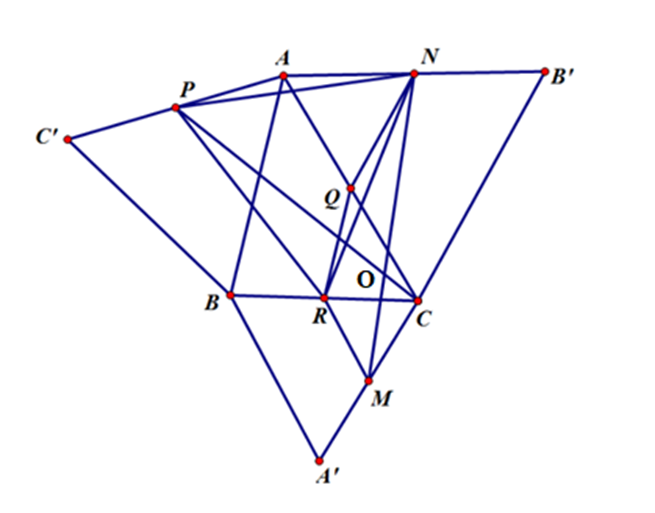
a) Gọi R là trung điểm của BC, Q là trung điểm của AC,
Xét tam giác ABC có R là trung điểm của BC, Q là trung điểm của AC,
Suy ra QR là đường trung bình của tam giác
Do đó QR // AB, \[QR = \frac{1}{2}AB\]
Suy ra \(\widehat {BAC} = \widehat {RQC}\) (hai góc đồng vị)
Vì tam giác ABC’ đều có P là trung điểm của AC’
Nên \(\widehat {ABC'} = \widehat {AC'B} = \widehat {BAC'} = 60^\circ \),
Mà \[QR = \frac{1}{2}AB\]
Suy ra AP = QR
Xét tam giác AB’C có N là trung điểm của B’A, Q là trung điểm của AC
Suy ra QN là đường trung bình
Do đó QN // CB’,
Suy ra \(\widehat {NQC} + \widehat {QCB'} = 180^\circ \)
Hay \(\widehat {NQC} = 180^\circ - \widehat {QCB'} = 180 - 60^\circ = 120^\circ \)
Vì tam giác AB’C đều có N là trung điểm của AB’
Nên \(\widehat {AB'C} = \widehat {ACB'} = \widehat {B'AC} = 60^\circ \),
Mà
Suy ra QN = AN
Ta có \(\widehat {NAP} = \widehat {NAC} + \widehat {CAB} + \widehat {BAP} = 60^\circ + \widehat {CAB} + 60^\circ = \widehat {CAB} + 120^\circ \)
\(\widehat {NQ{\rm{R}}} = \widehat {CQ{\rm{R}}} + \widehat {NQC} = \widehat {CQ{\rm{R}}} + 120^\circ \)
Lại có \(\widehat {BAC} = \widehat {RQC}\) (chứng minh trên)
Suy ra \(\widehat {NAP} = \widehat {NQR}\)
Xét tam giác ANP và tam giác QNR có
QN = AN (chứng minh trên)
\(\widehat {NAP} = \widehat {NQR}\) (chứng minh trên)
AP = QR (chứng minh trên)
Do đó DANP = DQNR (c.g.c)
Suy ra PN = NR, \(\widehat {ANP} = \widehat {QNR}\)
Xét tam giác ANQ có
Suy ra tam giác ANQ đều
Do đó \(\widehat {ANQ} = 60^\circ \)
Hay \(\widehat {ANP} + \widehat {PNQ} = 60^\circ \)
Mà \(\widehat {ANP} = \widehat {QNR}\)
Suy ra \(\widehat {QN{\rm{R}}} + \widehat {PNQ} = 60^\circ \)
Hay \(\widehat {PNR} = 60^\circ \)
Mặt khác NP = NR (chứng minh trên)
Suy ra tam giác PNR đều
Do đó RN = RP
Xét tam giác A’BC có R là trung điểm của BC, M là trung điểm của A’C
Suy ra RM là đường trung bình
Do đó RM // BA’,
Vì tam giác A’BC đều có R là trung điểm của BC
Nên \(\widehat {A'BC} = \widehat {A'CB} = \widehat {BA'C} = 60^\circ \),
Mà
Suy ra RC = RM
Ta có \(\widehat {P{\rm{R}}C} = \widehat {PRN} + \widehat {RNC} = 60^\circ + \widehat {RNC}\)
\(\widehat {N{\rm{RM}}} = \widehat {CRM} + \widehat {NRC} = 60^\circ + \widehat {NRC}\)
Suy ra \(\widehat {PRC} = \widehat {NRM}\)
Xét tam giác PRC và tam giác NRM có
PR = RN (chứng minh trên)
\(\widehat {PRC} = \widehat {NRM}\) (chứng minh trên)
RC = RM (chứng minh trên)
Do đó DPRC = DNRM (c.g.c)
Suy ra PC = NM (hai cạnh tương ứng)
b) Vì △PRC = △NRM (chứng minh câu a)
Nên \(\widehat {RPC} = \widehat {RNM}\) (hai góc tương ứng)
Xét tam giác PNO có \(\widehat {PNO} + \widehat {PON} + \widehat {OPN} = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {PNR} + \widehat {RNM} + \widehat {PON} + \widehat {OPN} = 180^\circ \)
Mà \(\widehat {RPC} = \widehat {RNM}\)
Suy ra \(\widehat {PON} = 180^\circ - \widehat {NP{\rm{R}}} - \widehat {PN{\rm{R}}} = 180^\circ - 60^\circ - 60^\circ = 60^\circ \)
Lại có \(\widehat {PON} = \widehat {MOC}\) (hai góc đối đỉnh)
Suy ra \(\widehat {MOC} = 60^\circ \)
Vậy \(\widehat {MOC} = 60^\circ \).
Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết MP = PN. Chọn câu đúng.
Cho tam giác ABC có AB = AC, gọi D là trung điểm của BC. Chứng minh
a) Tam giác ADB bằng tam giác ADC.
b) AD là tia phân giác của góc BAC.
c) AD vuông góc BC.
Cho DABC đều cạnh a. Gọi I là trung điểm BC.
a) Tính \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\).
b) Tính \(\left| {\overrightarrow {BA} - \overrightarrow {BI} } \right|\).
Bước 1: Gọi a, b, c, d lần lượt là tọa đọ của điểm A, B, C, D trên trục x’Ox. Ta có
\(\overline {AB} .\overline {C{\rm{D}}} \) = (b – a)(d – c) = bd – ad – bc + ac (1)
Bước 2: Tương tự \(\overline {AC} .\overline {{\rm{DB}}} \) = cb – ab – cd + ad (2)
Bước 3: Tương tự \(\overline {AD} .\overline {BC} \) = dc – ac – ba + ab (3)
Bước 4: Cộng (1), (2), (3) theo từng vế và rút gọn ta suy ra:
\(\overline {AB} .\overline {C{\rm{D}}} + \overline {AC} .\overline {DB} + \overline {A{\rm{D}}} .\overline {BC} = 0\)
Học sinh giải sai từ bước nào?
Cho bảng biến thiên hàm số y = f(x) như sau:
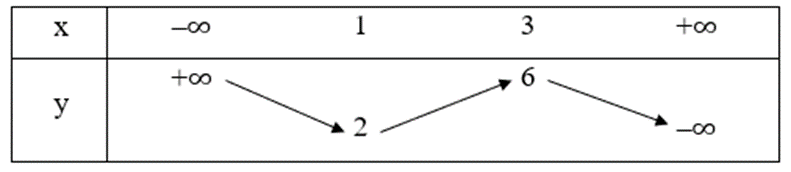
So sánh f(– 2021) và f(– 1); \(f\left( {\sqrt 3 } \right)\) và f(2).
Cho tam giác ABC có \(\widehat B = \widehat C\) . Tia phân giác của góc A cắt BC tại D. Chứng minh rằng:
a) Tam giác ADB bằng tam giác ADC
b) AB = AC.
Cho tam giác ABC có a = 8, b = 10, \(\widehat C = 60^\circ \). Độ dài cạnh c là
Tìm giá trị thực của tham số m khác 0 để hàm số y = mx2 – 2mx – 3m – 2 có giá trị nhỏ nhất bằng – 10 trên ℝ.
Tìm m để hàm số y = \(\sqrt {{x^2} + 4{\rm{x}} + m} \)có tập xác định là ℝ.
Cho A = (m; m + 1) ; B = (3; 5)
a) Tìm m để A hợp B là một khoảng. Xác định các khoảng đó.
b) A ∩ B ≠ ∅.
c) A ∩ B = ∅.
Cho tam giác đều ABC cạnh a, gọi G là trọng tâm. Khi đó giá trị \(\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right|\) là:
Rút gọn biểu thức sau
a) \(\sqrt {5 - 2\sqrt 6 } + \sqrt 2 \);
b) \(\sqrt {8 - 2\sqrt {15} } - \sqrt 5 \);
c) \(\sqrt {7 - 4\sqrt 3 } + 2\);
e) \(\sqrt {35 - 12\sqrt 6 } \);
g) \(\sqrt {7 - 3\sqrt 5 } \);
f) \(\sqrt {11 - 6\sqrt 2 } \).