Giải bởi Vietjack
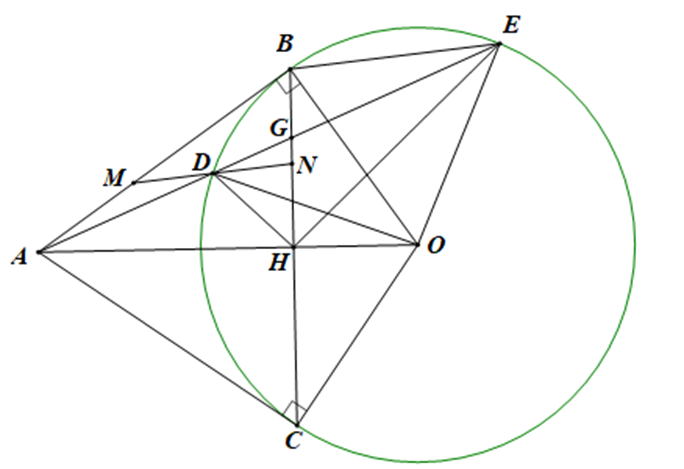
a) Vì AB, AC là tiếp tuyến của (O) nên AB ⊥ OB, AC ⊥ OC
Do đó \(\widehat {ABO} = \widehat {ACO} = 90^\circ \)
Suy ra A, B, O, C cùng thuộc đường tròn đường kính AO.
b) Xét (O) có AB, AC là hai tiếp tuyến cắt nhau tại A, suy ra AB = AC
Hay A thuộc trung trực của BC
Mà O thuộc trung trực của BC (vì OB = OC)
Suy ra AO là trung trực của BC
Do đó AO ⊥ BC.
Xét tam giác ABO vuông tại B có BH ⊥ AO
Suy ra OB2 = OH . OA (hệ thức lượng trong tam giác vuông)
Mà OB = OD (cùng là bán kính của (O)).
Suy ra OD2 = OH . OA.
Do đó \(\frac{{OD}}{{OA}} = \frac{{OH}}{{O{\rm{D}}}}\)
Xét tam giác OHD và tam giác ODA có
\(\frac{{OD}}{{OA}} = \frac{{OH}}{{O{\rm{D}}}}\) (Chứng minh trên)
\(\widehat {DOA}\) là góc chung
Suy ra (c.g.c)
c) Ta có OB2 = OH . OA (chứng minh câu b)
Mà OB = OE, suy ra OE2 = OH . OA
Do đó \(\frac{{OH}}{{OE}} = \frac{{OE}}{{OA}}\)
Xét tam giác OHE và tam giác OEA có
\(\frac{{OH}}{{OE}} = \frac{{OE}}{{OA}}\) (Chứng minh trên)
\(\widehat {EOA}\) là góc chung
Suy ra (c.g.c)
Do đó \(\widehat {EHO} = \widehat {A{\rm{E}}O}\) (hai góc tương ứng)
Mặt khác \(\widehat {DEO} = \widehat {EDO}\) (vì tam giác ODE cân tại O)
Suy ra \(\widehat {EHO} = \widehat {{\rm{ED}}O}\)
Xét tứ giác HDEO có \(\widehat {EHO} = \widehat {{\rm{ED}}O}\), mà hai góc này cùng nhìn cạnh EO trong tứ giác
Suy ra tứ giác HDEO nội tiếp
Do đó \(\widehat {DHA} = \widehat {AEO} = \widehat {OHE}\)
Suy ra \(\widehat {DHB} = \widehat {BHE}\) nên \(HB\) là tia phân giác của góc DHE.
Hay CB trùng với tia phân giác của góc DHE.
d) Gọi G là giao điểm của BC và AE
Do HG là tia phân giác của \(\widehat {DHE}\)nên \(\frac{{{\rm{GD}}}}{{{\rm{GE}}}} = \frac{{HD}}{{HE}}\) (1)
Mà HA ⊥ HG
Suy ra HA là tia phân giác ngoài của tam giác HED
Do đó \(\frac{{A{\rm{D}}}}{{A{\rm{E}}}} = \frac{{H{\rm{D}}}}{{HE}}\) (2)
Từ (1) và (2) suy ra \(\frac{{{\rm{GD}}}}{{{\rm{GE}}}} = \frac{{A{\rm{D}}}}{{A{\rm{E}}}}\left( { = \frac{{H{\rm{D}}}}{{HE}}} \right)\) (3)
Xét DABE có DM // BE nên \(\frac{{M{\rm{D}}}}{{BE}} = \frac{{A{\rm{D}}}}{{A{\rm{E}}}}\) (hệ quả định lí Thales) (4)
Xét DGBE có DN // BE nên \(\frac{{{\rm{ND}}}}{{BE}} = \frac{{{\rm{GD}}}}{{{\rm{GE}}}}\) (hệ quả định lí Thales) (5)
Từ (3), (4) và (5), suy ra \(\frac{{{\rm{MD}}}}{{BE}} = \frac{{{\rm{ND}}}}{{{\rm{BE}}}}\)
Hay MD = ND
Do đó D là trung điểm của MN
Vậy D là trung điểm của MN.
Cho tam giác ABC vuông tại A, đường cao AH. Qua H kẻ các đường thẳng song song với AB và AC lần lượt cắt AC tại E, AB tại D.
a) Chứng minh rằng: Tứ giác ADHE là hình chữ nhật.
b) Gọi M, N lần lượt là trung điểm của BH và CH. Biết AB = 6 cm; AC = 8 cm. Tính BC, DM, DM + EN?
c) Chứng minh rằng: Tứ giác DMNE là hình thang.
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN).
Chứng minh các hệ thức
a) \(1 + {\tan ^2}a = \frac{1}{{{\rm{co}}{{\rm{s}}^2}a}}\);
b) \(1 + {\cot ^2}a = \frac{1}{{{\rm{si}}{{\rm{n}}^2}a}}\);
c) \(\frac{{\cos a}}{{1 - \sin a}} = \frac{{1 + \sin a}}{{\cos a}}\).
Cho hình vuông ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF.
a) Chứng minh tam giác EDF vuông cân.
b) Gọi I là trung điểm của EF. Chứng minh BI = DI.
c) Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh O, C, I thẳng hàng.
Phương trình \(\sqrt 3 \sin x - cosx = 1\) tương đương với phương trình nào sau đây?
Cho tam giác ABC nhọn. Chứng minh rằng BC2 = AB2 + AC2 – 2AB.AC.cosA.
Cho tam giác ABC nhọn, BD vuông góc với AC, D thuộc AC, CE vuông góc với AB, E thuộc AB, BD cắt CE tại I. Chứng minh góc BIC bù góc A.
Cho đường tròn tâm O bán kính R = 2,5 cm và dây AB di động, sao cho AB = 4 cm. Hỏi trung điểm H của AB di động trên đường nào?
Cho tam giác ABC cân tại A \(\left( {\widehat A < 90^\circ } \right)\), đường cao AH. Kẻ HK ⊥ AC (K ∈ AC).
a) Tính HC, HK, \(\widehat C\) nếu AH = 20 cm, AC = 25 cm.
b) Qua B kẻ đường thẳng song song với AH, đường thẳng này cắt AC tại điểm E. Kẻ BD ⊥ AC (D ∈ AC). Chứng minh \(B{H^2} = \frac{{C{\rm{D}}.CE}}{4}\).
c) Gọi O là giao điểm của BD và AH. Chứng minh \(\frac{{BO}}{{DO}} = \frac{{A{\rm{E}}}}{{A{\rm{D}}}}\).
d) Kẻ KF ⊥ BC (F ∈ BC). Chứng minh CF = AC. sin3E.
Cho tam giác ABC với AB = AC. Lấy I là trung điểm BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm M sao cho CN = BM. Chứng minh:
a) \(\widehat {ABI} = \widehat {ACI}\)và AI là tia phân giác của góc BAC.
b) AM = AN.
c) AI vuông góc với BC.
Cho tam giác ABC với AB = AC. Lấy I là trung điểm BC. Trên tia BC lấy điểm N, trên tia CB lấy điểm M sao cho CN = BM. Chứng minh:
a) \(\widehat {ABI} = \widehat {ACI}\)và AI là tia phân giác của góc BAC.
b) AM = AN.
c) AI vuông góc với BC.
Một ô tô chạy 100km hết 13 lít xăng. Hỏi cần bao nhiêu xăng khi ô tô chạy quãng đường 300 000 m?
