Cho ∆ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE.
a. Chứng minh rằng BE = CD.
b. Chứng minh rằng \(\widehat {ABE} = \widehat {ACD}\).
c. Gọi K là giao điểm của BE và CD. ∆KBC là tam giác gì? Vì sao?
Giải bởi Vietjack
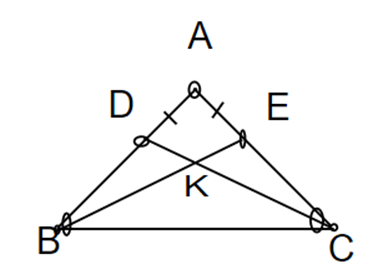
a. Ta có AB = AD + DB, AC = AE + EC mà AB = AC (vì ∆ABC cân tại A)
AD = AE (giả thiết) ⇒ DB = EC
Xét ∆BEC và ∆CDB có: DB = EC (chứng minh trên)
\(\widehat {ABC} = \widehat {ACB}\) (Vì ∆ABC cân tại A)
BC là cạnh chung
\( \Rightarrow \Delta BEC = \Delta CDB\left( {c.g.c} \right) \Rightarrow BE = CD\) (2 cạnh tương ứng)
b. Vì \(\Delta BEC = \Delta CDB\) (chứng minh trên) \( \Rightarrow \widehat {EBC} = \widehat {DCB}\) (2 góc tương ứng)
Ta có: \(\widehat {ABC} = \widehat {ABE} + \widehat {EBC}\), \(\widehat {ACB} = \widehat {ACD} + \widehat {DCB}\)
Mà \(\widehat {ABC} = \widehat {ACB}\) (Vì \(\Delta ABC\)cân tại A)
\(\widehat {EBC} = \widehat {DCB}\) (chứng minh trên)
\( \Rightarrow \widehat {ABE} = \widehat {ACD}\) (điều phải chứng minh)
c. Xét ∆KBC có: \(\widehat {EBC} = \widehat {DCB}\) (chứng minh trên)
⇒ ∆KBC là tam giác cân tại K.
Cho \(\cos x = \frac{2}{{\sqrt 5 }},0 < x < \frac{\pi }{2}\). Tính các giá trị lượng giác của góc x.
Một đoạn dây dẫn được uốn thành hình chữ nhật, có các cạnh a = 16 cm, b = 30 cm, trong đó có dòng điện cường độ I = 6A chạy qua. Xác định cảm ứng từ tại tâm hình chữ nhật ?
Trên khoảng \(\left( {\frac{\pi }{2};2\pi } \right)\), phương trình \(\cos \left( {\frac{\pi }{6} - 2\pi } \right) = \sin x\) có bao nhiêu nghiệm ?
Cho ∆ABC có \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và a = 10. Tính chu vi tam giác.
Cho ∆ABC vuông tại A có đường cao AH. Kẻ HE, HF vuông góc với AB, AC. Chứng minh rằng: \(\frac{{EB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\).
Cho ∆ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm A, bán kính AH, kẻ các tiếp tuyến BD, CE với đường tròn tâm A (D, E là các tiếp điểm khác H). Chứng minh rằng:
a. 3 điểm D, A, E thẳng hàng.
b. DE tiếp xúc với đường tròn có đường kính BC.
Cho ∆ABC nhọn, đường cao AH. Kẻ HD ⊥ AB, HE ⊥ AC.
a.Chứng minh AD.AB = AE.AC.
b. Chứng minh \(\frac{{AD}}{{BD}} = \frac{{A{H^2}}}{{B{H^2}}}\).Một đội công nhân có 25 người nhận sửa xong một quãng đường trong 9 ngày. Hỏi muốn làm xong quãng đường đó trong 5 ngày thì cần thêm bao nhiêu người ?(mức làm của mỗi người như nhau).
Cho ∆ABC vuông tại A, M là trung điểm của BC, D, E lần lượt là hình chiếu của M trên AB và AC.
a) Tứ giác ADME là hình gì, tại sao?
b) Chứng minh DE = \(\frac{1}{2}\)BC.
c) Gọi P là trung điểm của BM, Q là trung điểm của MC, chứng minh tứ giác DPQE là hình bình hành. Từ đó chứng minh: tâm đối xứng của hình bình hành DPQE nằm trên đoạn AM.
d) Tam giác vuông ABC ban đầu cần thêm điều kiện gì để hình bình hành DPQE là hình chữ nhật?
Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{{x^4} + 2{x^3}y + {x^2}{y^2} = 2x + 9}\\{{x^2} + 2xy = 6x + 6}\end{array}} \right.\).
Cho đường tròn (O; R) đường kính AB. Kẻ tiếp tuyến Ax, lấy P trên Ax (AP > R). Từ P kẻ tiếp tuyến PM với (O).
a, Chứng minh bốn điểm A, P, M, O cùng thuộc một đường tròn.
b, Chứng minh BM // OP.
c, Đường thẳng vuông góc với AB tại O cắt tia BM tại N. Chứng minh tứ giác OBNP là hình bình hành.
d, Giả sử AN cắt OP tại K; PM cắt ON tại I; PN cắt OM tại J. Chứng minh I, J, K thẳng hàng.
Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt cạnh AB, AC theo thứ tự ở D và E.
a. Chứng minh rằng CD ⊥ AB, BE ⊥ AC.
b. Gọi K là giao điểm của BE, CD. Chứng minh AK ⊥ BC.
Cho hình bình hành ABCD. E, F lần lượt là trung điểm của AB và CD.
a. Tứ giác DEBF là hình gì? Vì sao?
b. Chứng minh 3 đường thẳng AC, BD, EF đồng quy.
c. Gọi giao điểm của AC với DE và BF theo thứ tự là M, N. Chứng minh tứ giác EMFN là hình bình hành.
Cho ∆MNP. Gọi D, E, F lần lượt là trung điểm của MN, NP, PM.
a. Chứng minh tứ giác MDEF là hình bình hành.
b. ∆MNP có điều kiện gì thì tứ giác MDEF là hình chữ nhật.
Cho ∆ABC nhọn nội tiếp đường tròn (O, R). Biết AB = \(R\sqrt 3 \) , AC = \(R\sqrt 2 \) . Tính các góc tam giác đó.
