Cho ∆ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AC, AB lần lượt tại I, K. So sánh các cung nhỏ BI và cung nhỏ CK.
 Giải bởi Vietjack
Giải bởi Vietjack
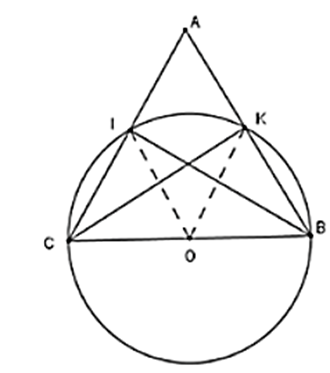
Xét các tam giác ∆IBC và ∆KBC: có BC là đường kính của (O) và I, K ∈ (O)
Nên ∆IBC vuông tại I và ∆KBC vuông tại K.
Xét 2 tam giác vuông ∆IBC và ∆KBC, ta có: BC chung, \(\widehat {ABC} = \widehat {ACB}\)(do ∆ABC cân)
⇒ ∆IBC = ∆KCB (ch – gn) ⇒ IB = CK
⇒ ∆COK = ∆IOB (c.c.c) ⇒ \(\widehat {COK} = \widehat {IOB}\)
⇒ Số đo 2 cung nhỏ CK và BI bằng nhau.
Cho đường tròn (O; R) và dây AB = 1,6R. Vẽ 1 tiếp tuyến song song AB cắt các tia OA, OB theo thứ tự tại M và N. Tính \({S_{_{\Delta OMN}}}\) theo R.
Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A ≠ B và C). Qua O, kẻ tia Ox // AC, tia Ox cắt AB tại D.
a. Chứng minh: OD ⊥ AB và từ đó suy ra D là trung điểm của AB.
b. Tiếp tuyến tại B của (O) cắt tia Ox tại E. Chứng minh: EA cũng là tiếp tuyến của (O).
c. Tia CA cắt tia BE tại F. Chứng minh: Tia CE đi qua trung điểm I của đường cao AH.
Cho hình bình hành ABCD có AD = 2AB. Từ C kẻ CE ⊥ AB, nối E với trung điểm M của AD, từ M kẻ MF ⊥ CE, MF ∩ BC = N.
a. Hỏi MNCD là hình gì?
b. ∆EMC là tam giác gì?
c. Chứng minh \(\widehat {BAD} = 2\widehat {AEM}\)
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.
Cho hình chữ nhật ABCD, vẽ ∆AEC vuông tại E. Chứng minh năm điểm A, B, C, D, E cùng thuộc một đường tròn.
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và đáy bằng 30°. Thể tích khối chóp S.ABC bằng ?
Cho đường tròn tâm O, đường kính AB = 10 cm. Trên đường tròn tâm O lấy điểm C sao cho AC = 6 cm . Kẻ CH ⊥ AB tại H.
a. So sánh dây AB và dây BC.
b. ∆ABC là tam giác gì? Vì sao?
c. Từ O kẻ OI ⊥ BC tại I. Tính độ dài OI.
d. Tiếp tuyến tại A của đường tròn (O) cắt tia BC tại E.
Chứng minh CE × CB = AH × AB.
Cho hình bình hành ABCD và điểm M tùy ý.
Chứng minh rằng \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \).
Cho ∆ABC. Chứng minh rằng: \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{4S}}\).
Trong mặt phẳng tọa độ (Oxy), cho phép biến hình F có biểu thức tọa độ \(x' = \frac{{ - 3x + 4y}}{5};y' = \frac{{4x + 3y}}{5}\). Ảnh của \(\Delta :x + y = 0\) qua phép biến hình F là ?
Cho ∆ABC. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Cho diện tích ∆ABC bằng 24 cm2. Tính diện tích ∆MNP.
Cho hình bình hành ABCD và điểm E bất kì.
Chứng minh \(\overrightarrow {AB} + \overrightarrow {CE} + \overrightarrow {AD} = \overrightarrow {AE} \).
Cho hình chóp S.ABCD có AD không song song với BC, lấy I ∈ SA so cho SA = 3IA, lấy J ∈ SC; M là trung điểm SB.
a. Tìm giao tuyến của (SAD) và (SBC).
b. Tìm giao điểm E của AB và (IJM).
c. Tìm giao điểm F của BC và (IJM).
d. Tìm giao điểm N của SD và (IJM).
e. Gọi H = MN ∩ BD. Chứng minh rằng: H, E, F thẳng hàng.