Giải bởi Vietjack
Lời giải:
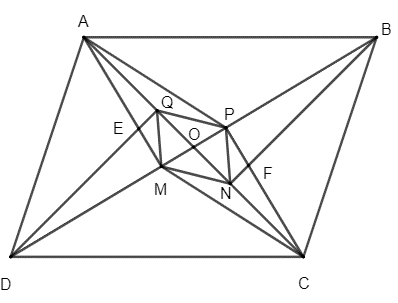
Vì O là giao hai đường chéo của hình bình hành ABCD nên O là trung điểm của AC và BD.
Xét ΔAMO vuông tại M và ΔCPO vuông tại P có
OA = OC (O là trung điểm AC); \(\widehat {AOM} = \widehat {COP}\) (đối đỉnh)
Do đó: ΔAMO = ΔCPO (cạnh huyền – góc nhọn)
⇒ OM = OP hay O là trung điểm của PM.
Xét ΔDQO vuông tại Q và ΔBNO vuông tại N có
OD = OB (O là trung điểm của BD); \(\widehat {DOQ} = \widehat {BON}\) (đối đỉnh)
Do đó: ΔDQO = ΔBNO (cạnh huyền – góc nhọn)
⇒ OQ = ON hay O là trung điểm của QN
Xét tứ giác AMCP có:
O là trung điểm của AC; O là trung điểm của MP
Do đó: AMCP là hình bình hành.
Xét tứ giác MNPQ có
O là trung điểm của MP; O là trung điểm của NQ.
Do đó: MNPQ là hình bình hành.
Cho hình thang cân ABCD (AB // CD, AB < CD). Gọi O là giao điểm của AD và BC; gọi E là giao điểm của AC và BD. Chứng minh:
a) ∆AOB cân tại O.
b) ∆ABD = ∆BAC.
c) EC = ED.
d) OE là đường trung trực chung của AB và CD.
Cho ∆ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng:
a. AC = EB và AC // BE.
b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho: AI = EK. Chứng minh: I, M, K thẳng hàng.
c. Từ E kẻ EH ⊥ BC (H ∈ BC). Biết \(\widehat {HBE}\)= 50\(^\circ \), \(\widehat {MEB}\) = 25\(^\circ \), tính \(\widehat {HEM}\) và \(\widehat {BME}\).
Cho ∆ABC vuông tại A, có phân giác AD.
Chứng minh rằng: \(\frac{1}{{AB}} + \frac{1}{{AC}} = \frac{{\sqrt 2 }}{{AD}}\).
Viết phương trình đường thẳng d trong các trường hợp sau:
a. d đi qua M(–2; 5) và vuông góc với \({d_1}:y = - \frac{1}{2}x + 2\).
b. d // \({d_1}:y = - 3x + 4\) và đi qua giao của 2 đường thẳng\({d_2}:y = 2x - 3;{d_3}:y = 3x - \frac{7}{2}\).
Cho đường tròn (O), đường kính AB = 2R, dây MN vuông góc với dây AB tại I sao cho IA < IB. Trên đoạn MI lấy điểm E (E ≠ M, I). Tia AE cắt đường tròn tại điểm thứ hai là K.
a. Chứng minh tứ giác IEKB nội tiếp.
b. Chứng minh ∆AME, AKM đồng dạng với nhau và \(A{M^2} = AE.AK\).
c. Chứng minh: \(AE.AK + BI.BA = 4{R^2}\).
d. Xác định vị trí điểm I sao cho chu vi ∆MIO đạt GTLN.
