Cho bộ nguồn gồm 3 pin giống nhau ghép nối tiếp mỗi pin có \(\xi = 2V,r = 0,5\Omega \) mắc trong mạch kín có \({R_1} = 1,5\Omega \); \({R_2} = {R_3} = 2\Omega \); \(R{ & _4} = 1\Omega \).
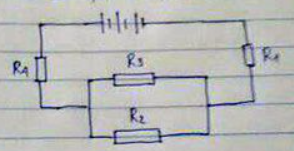
Tính
a) Cường độ dòng điện qua mạch chính và công suất qua R1.
b) Công suất của nguồn.
c) Hiệu suất của mạch.
Giải bởi Vietjack
Lời giải:
\[{R_{1\,}}nt\,({R_2}\parallel {R_3})\,nt\,{R_4}\]
a) \[{\xi _{bo}} = 3.2 = 6(V)\]
\[{r_{bo}} = 3.0,5 = 1,5(V)\]
Có \[{R_{23}} = \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = 1(\Omega )\]
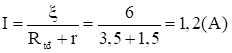
\[{P_1} = I_1^2.{R_1} = {1,2^2}.1,5 = 2,16\,({\rm{W}})\]
b) \[{P_{\;nguon}} = \xi .I = 6.1,2 = 7,2\,\,({\rm{W}})\]
c) \[\frac{{{A_{c\'o {\rm{ }}\'i ch}}}}{{{A_{tp}}}} = \frac{{U.I.t}}{{\xi .I.t}} = \frac{U}{\xi } = \frac{{I.{R_{td}}}}{{I({R_{td}} + r)}} = \frac{{{R_{td}}}}{{{R_{td}} + r}}\]
\[ \Rightarrow H = \frac{{{A_{c\'o {\rm{ }}\'i ch}}}}{{{A_{tp}}}}.100\% = \frac{{{R_{td}}}}{{{R_{td}} + r}}.100\% = 70\% \]
Một con lắc đơn có chiều dài l = 1 m được kéo ra khỏi vị trí cân bằng một góc \[{\alpha _{0\;}} = {5^{o\;}}\]so với phương thẳng đứng rồi thả nhẹ cho vật dao động.
Cho \[g\; = \;{{\rm{\pi }}^2}\; = \;10m/{s^2}\]. Vận tốc của con lắc khi về đến vị trí cân bằng có giá trị là:
Dựa vào công thức tính áp suất \[p = \frac{F}{S}\], hãy chứng minh công thức \[p = d.h\]Trong đó: p là áp suất ở đáy cột chất lỏng
D là trọng lượng riêng của chất lỏng
H là chiều cao cột chất lỏng
Với p tính bằng Pa, d tính bằng N/m3, h tính bằng m
Một điện trường đều cường độ 4000 V/m, có phương song song với cạnh huyền BC của một tam giác vuông ABC có chiều từ B đến C, biết AB = 6 cm, AC = 8 cm. Tính hiệu điện thế giữa hai điểm BA:
