 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
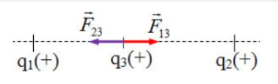
Để \[{q_3}\]nằm cân bằng (lực điện tác dụng lên \[{q_3}\]bằng 0) thì hai vecto lực \[{F_1}\] do \[{q_1}\] tác dụng lên \[{q_3}\]và \[{F_2}\] do \[{q_2}\]tác dụng lên \[{q_3}\] phải ngược chiều và cùng độ lớn nên C nằm trên đường thẳng AB
Vì \[{q_1},{q_2}\]cùng dấu nên C nằm trong đoạn \[AB \Rightarrow {r_1} + {r_2} = AB\]
\[{F_1} = {F_2} \Leftrightarrow \frac{{{q_1}}}{{r_1^2}} = \frac{{{q_2}}}{{r_2^2}} \Leftrightarrow \frac{1}{{r_1^2}} = \frac{4}{{r_2^2}} \Leftrightarrow {r_2} = 2{r_1}\]\[ \Rightarrow 3{r_1} = 9 \Rightarrow {r_1} = 3cm\]
Một con lắc đơn có chiều dài l = 1 m được kéo ra khỏi vị trí cân bằng một góc \[{\alpha _{0\;}} = {5^{o\;}}\]so với phương thẳng đứng rồi thả nhẹ cho vật dao động.
Cho \[g\; = \;{{\rm{\pi }}^2}\; = \;10m/{s^2}\]. Vận tốc của con lắc khi về đến vị trí cân bằng có giá trị là:
Một điện trường đều cường độ 4000 V/m, có phương song song với cạnh huyền BC của một tam giác vuông ABC có chiều từ B đến C, biết AB = 6 cm, AC = 8 cm. Tính hiệu điện thế giữa hai điểm BA:
Dựa vào công thức tính áp suất \[p = \frac{F}{S}\], hãy chứng minh công thức \[p = d.h\]Trong đó: p là áp suất ở đáy cột chất lỏng
D là trọng lượng riêng của chất lỏng
H là chiều cao cột chất lỏng
Với p tính bằng Pa, d tính bằng N/m3, h tính bằng m